Week 9

• Problem (posted October 30th)

  This week we look at a geometric inequality.

  Points $D$ and $E$ are given on the sides $AB$ and $AC$ of a triangle $ABC$ in such a way that $DE$ is parallel to $BC$ and tangent to the incircle of $\Delta ABC$. Prove that $$DE \leq \frac{1}{8} \left(AB+AC+BC \right).$$

• Solution (posted November 6th)

  Problem 2 of the Italian Team Selection Contest, 1999 which appeared in Crux Mathematicorum [2002:356-357]. We present the solution by Toshio Seimiya which appeared at [2004:492].

  

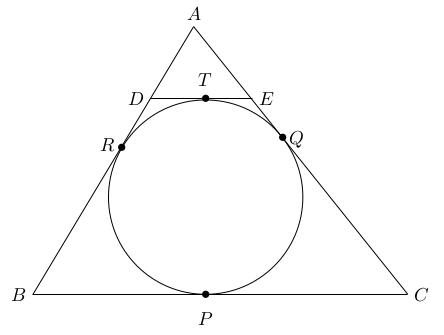
  We set $BC=a, AC=b, AB=c$. Let the incircle touch $BC, CA$ and $AB$, at $P,Q,R,$ respectively. We also denote by $T$ the point where $DE$ is tangent to the circle.

  Since $DE \parallel BC$ we have $\Delta ADE \sim \Delta ABC$ and hence

  (4)	$\frac{AD+DE+EA}{AB+BC+CA}=\frac{DE}{BC}=\frac{DE}{a}.$

  Next, the tangents from $D$ to the circle are congruent, and the tangents from $E$ to the circle are congruent. Therefore

  $DT$	$=DR$
  $ET$	$=EQ.$

  We therefore have

  (5)	$AD+DE+EA=AQ+AR.$

  Next, using again that the tangents from $A,B$ and $C$ respectively are congruent, we get

  $AR$	$=AQ$
  $BR$	$=BP$
  $CQ$	$=CP.$

  Therefore $$b+c-a=AR+BR+AQ+CQ-BP-CP=AR+AQ.$$

  Therefore, by (5) we have $$AD+DE+EA=AQ+AR=b+c-a.$$

  Plugging this into (4) we get $$\frac{b+c-a}{b+c+a}=\frac{DE}{a}.$$

  Therefore $$DE=\frac{a(b+c-a)}{(b+c+a)}.$$

  Then

  $\frac{1}{8} \left( AB+BC+CA \right)-DE$	$= \frac{1}{8}(a+b+c)- \frac{a(b+c-a)}{(b+c+a)}$
  	$=\frac{1}{8(a+b+c)} \left( (a+b+c)^2-8a(b+c-a) \right)$
  	$=\frac{1}{8(a+b+c)} \left( a^2+2a(b+c)+(b+c)^2-8a(b+c)+8a^2 \right)$
  	$=\frac{1}{8(a+b+c)} \left( 9a^2-6a(b+c)+(b+c)^2 \right)$
  	$=\frac{1}{8(a+b+c)} \left( 3a- (b+c) \right)^2 \geq 0.$

  Therefore, $$DE \leq \frac{1}{8} \left(AB+AC+BC \right).$$

Week 8

• Problem (posted October 23rd)

  This week we look at an equation in primes.

  Find all prime numbers $p$ and $q$ such that $$p^2-p+1=q^3.$$

• Solution (posted October 30th)

  Problem 4 of the 25^th Albanian Math Olympiad, Test 1, which appeared in Crux Mathematicorum [2007:278-279]. We present the solution by Titu Zvonaru which appeared at [2008:220].

  We prove that the only solution is $p=19, q=7$ giving $$19^2-19+1=343=7^3.$$

  Let us start by observing that $$q^3 = p^2-p+1 < p^2 < p^3 \,,$$ and hence $q < p$.

  We can rewrite the equation as

  (2)	$p(p-1)=(q-1)(q^2+q+1).$

  Since $p$ is prime, (2) implies $p|q-1$ or $p|q^2+q+1$. We cannot have $p|q-1$ as $p>q>q-1>0$, and therefore, there must exists an integer $k$ such that

  (3)	$q^2+q+1=pk.$

  Combining (2) and (3) we get $$p-1=k(q-1)$$ and hence $$p=k(q-1)+1.$$

  Therefore, by (3) we get $$q^2+q+1=k^2q-k^2+k.$$

  This means that $q$ is a solution to the quadratic equation $$q^2+(1-k^2)q+(k^2-k+1)=0.$$

  Since $q$ is an integer, and the equation has integer coefficients, the discriminant $$\Delta= (k^2-1)^2-4(k^2-k+1) \,,$$ is a perfect square.

  Finally, as $k$ is a positive integer, we have $\Delta < (k^2-1)^2$ and $\Delta$ and $(k^2-1)^2$ have the same parity. It follows that $\Delta \leq(k^2-3)^2$.

  Therefore

  $(k^2-1)^2-4(k^2-k+1)$	$\leq (k^2-3)^2$
  $k^4-2k^2+1-4k^2+4k-4$	$\leq k^4-6k^2+9$
  $4k$	$\leq 12$
  $k$	$\leq 3.$

  Since $k$ is a positive integer, $k \in \{1 ,2 , 3 \}$.

  Now, $k=1$ and $k=2$ lead to $\Delta=-4$ and $\Delta=-3$, respectively, which is not possible. So the only possibility is $k=3$ which leads to $\Delta=36$ and $$q=\frac{8 \pm 6}{2}.$$

  Since $q$ is prime, $q=7$ and $$p=\frac{q^2+q+1}{k}=\frac{57}{3}=19.$$

  Therefore $$p=19 \,;\, q=7.$$

Week 7

• Problem (posted October 16th)

  This week we look at a question about constructing rectangles from a given shape. This type of construction is sometimes called a "tiling".

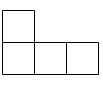
  Prove that an $m \times n$ rectangle can be constructed by using copies of the following shape (without overlap) if and only if $m,n >1$ and $8 | mn$.

  

• Solution (posted October 23rd)

  Problem 5 of the 2000 Korean Math Olympiad, which appeared in Crux Mathematicorum [2003:22-23]. We present the solution by Pierre Bornsztein which appeared at [2005:99-100], slightly modified.

  We will call a figure of the given shape a "tetramino".

  We first prove that if an $m \times n$ rectangle can be constructed by using tetraminoes then $m,n >1$ and $8|mn$. The claim that $m,n >1$ is clear.

  Since the rectangle has area $mn$ and a tetramino has an area of $4$ we get that $mn=4k$ where $k$ is the number of tetraminos. We show next that $k$ is even.

  Let us colour the rows of the $m \times n$ rectangle with black and white in an alternating manner, such that the odd numbered rows are all white and the even number rows are all black.

  Since $4|mn$, at least one of $m$ or $n$ must be even, and hence the number of unit white squares must be even (and the number of unit black squares must be even too).

  Now, regardless of its position and orientation on the board, it is clear that a tetramino must contain either one or three white squares. We will denote by $t$ the number of tetraminos which contain three white square. Then, the remaining $k-t$ tetraminos must contain one white square each.

  Since the number of white squares is even, we get that $$3t+(k-t)=k-2t \mbox{ is even }.$$

  This implies that $k$ is even and hence, $mn=4k$ is divisible by $8$.

  Next, we prove that, if $m,n >1$ and $8|mn$ then an $m \times n$ rectangle can be constructed from tetraminos.

  Let us observe first that a $2 \times 4$ and a $3 \times 8$ board can be constructed from tetraminos, as shown below:

  

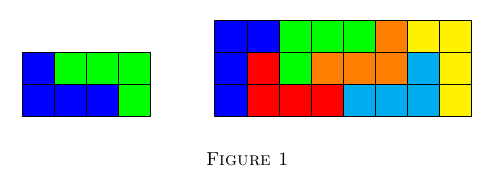
  Now, by eventually rotating the board by $90^\circ$ we can assume that either (i) $4|n$ and $2|m$ or (ii) $8 |n$.

  In the case (i) we can construct the rectangle by using $\frac{mn}{8}$ copies of the $4 \times 2$ rectangle in Figure 1.

  Let us now discuss the case $8|n$.

  If $m$ is even, then we are in situation (i), and we can easily construct the board from $\frac{mn}{8}$ copies of the $4 \times 2$ rectangle in Figure 1.

  If $m$ is odd, since $m \neq 1$ we have $m \geq 3$. Then, $m-3=2k$ for some integer $k \geq 0$.

  Now, since $8 |n$ we can construct a $3 \times n$ rectangle from copies of the $3 \times 8$ rectangle in Figure 1.

  We can also construct a $2 \times n$ rectangle from copies of the $2 \times 4$ rectangle in Figure 1.

  Therefore, by using a $3 \times n$ rectangle and $k$ copies of $2 \times n$ rectangles, we can construct an $m \times n$ rectangle.

Week 6

• Problem (posted October 9th)

  This week we will look at a geometry problem.

  Let $ABC$ be an acute-angled triangle with $\angle B = \angle C$. Let $O$ be the circumcentre and let $H$ be the orthocentre of $\Delta ABC$. Prove that the centre of the circle $BOH$ lies on $AB$.

• Solution (posted October 16th)

  Problem 2 of the 2008/9 British Math Olympiad, Round 2, which appeared in Crux Mathematicorum [2011:352-353]. We present the solution by Oliver Geupel which appeared at [2012:270].

  

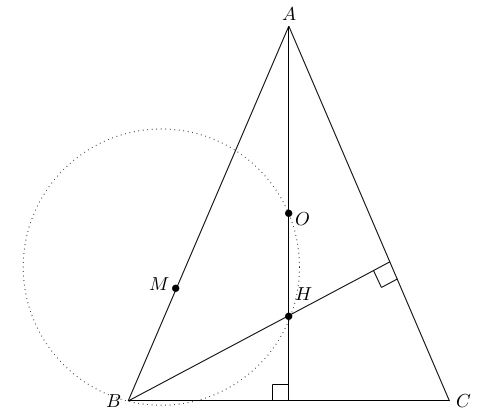
  Since $AC$ is perpendicular to the altitude $BH$, we have $$\angle ABH = 90^\circ - \angle A.$$

  Let $M$ be the centre of the circle $BOH$. Then $$\angle MBH = 90^\circ - \frac12 \angle BMH = 90^\circ - \angle BOH.$$

  Since $\angle B = \angle C$, it holds $$\angle BOH = \frac12 \angle BOC = \angle A.$$

  We deduce that $$\angle ABH = \angle MBH,$$ that is, the points $A$, $B$, and $M$ are collinear.

Week 5

• Problem (posted October 2nd)

  This week we look at a functional equation.

  Denote by $\mathbb{Q}$ the set of rational numbers. Find all functions $f: \mathbb{Q} \to \mathbb{Q}$ such that

  (1)	$f\left(x+f(y)\right)=y+f(x) \qquad \forall x,y \in \mathbb{Q}.$

• Solution (posted October 9th)

  Problem 8 of the 15^th Irish Mathematical Olympiad, which appeared in Crux Mathematicorum [2005:437-439]. We present the solution by Mohammed Aassila which appeared at [2007:33].

  Setting $x=0$ in (1) we get $$ f(f(y))=y+f(0) \qquad \forall y \in \mathbb{Q}. $$

  We claim that $f$ is a one-to-one function. Indeed, if $f(a)=f(b)$ then $$ a+f(0)=f(f(a))=f(f(b))=b+f(0) \,,$$ and hence, $a=b$.

  Next, setting $y=0$ in (1) we get $$f(x+f(0))=f(x).$$

  Since $f$ is one-to-one, we get that $x+f(0)=x$ and hence $$f(0)=0.$$

  Therefore, we also have $$f(f(y))=y \qquad \forall y \in \mathbb{Q}.$$

  Next, replacing $y$ by $f(y)$ in (1), and using $f(f(y))=y$ we get $$f(x)+f(y)=f(x+f(f(y))=f(x+y) \qquad \forall x, y \in \mathbb{Q}.$$

  This is the well known Cauchy Functional Equation, and implies that, with $a=f(1) \in \mathbb{Q}$, we have $f(x)=ax \, \forall x \in \mathbb{Q}$.

  Next, since $f(f(y))=y \, \forall y \in \mathbb{Q}$ we get $a=\pm 1$.

  Therefore, there are only two possible solutions to this equation: $f(x)=x \, \forall x \in \mathbb{Q}$ and $f(x)=-x \, \forall x \in \mathbb{Q}$.

  It is easy to check that $f(x)=x$ and $f(x)=-x$ are indeed solutions to (1).

  Note: For the unfamiliar reader, we include below the Cauchy Functional Equation.

  Let $f: \mathbb Q \to \mathbb Q$ be so that $$f(x+y)=f(x)+f(y) \qquad \forall x,y \in \mathbb Q$$ and let $a:=f(1)$.

  Since $f(x+y)=f(x)+f(y)$, an easy induction argument shows that $f(nx)=nf(x) \, \forall x \in \mathbb Q, n \in \mathbb N$. Also, as $$ 0=f(0)=f(x-x)=f(x)+f(-x) \,,$$ it follows that $f$ is an odd function and hence $$f(nx)=nf(x) \qquad \forall x \in \mathbb Q, n \in \mathbb Z.$$

  Let $x \in \mathbb Q$ be arbitrary, and write $x= \frac{m}{n}$ with $m,n \in \mathbb Z$ and $n >0$. Then, $$a=f(1)=f(n \cdot \frac{1}{n})=n f(\frac{1}{n}) \Rightarrow f(\frac{1}{n})=\frac{a}{n} \,,$$ and hence $$f(x)=f(\frac{m}{n})=f(m \cdot \frac{1}{n})=m f(\frac{1}{n}) =m \frac{a}{n}=ax.$$

  This shows that $f(x)=ax$ for all $x \in \mathbb Q$.

Week 4

• Problem (posted September 25th)

  This week we look at a polynomial with integer coefficients.

  Given $n$ distinct integers $m_1,...,m_n$, prove that there exists a polynomial $P(X)$ of degree $n$ with integer coefficients, which satisfies the following two conditions:

  1. $P(m_k)=-1$ for all $1 \leq k \leq n$.
  2. $P(X)$ is irreducible in $\mathbb{Z}[X]$, that is $P(X)$ cannot be written as the product of two non-constant polynomials with integer coefficients.

• Solution (posted October 2nd)

  Problem 4 of the 4^th Mathematical Olympiad of Republic of China (Taiwan), which appeared in Crux Mathematicorum [1998:322-323]. We present the solution by Pierre Bornsztein which appeared at [2000:75].

  It is easy to see that $$ P(X)=(X-m_1)(X-m_2)..(X-m_n)-1 $$ has integer coefficients and degree $n$. To complete the proof we show that $P(X)$ satisfies (ii).

  Assume by contradiction that we can find $Q,R \in \mathbb{Z}[X]$ of degree at most $n-1$ such that $$ P(X)=Q(X)\cdot R(X). $$

  Then, for each $1 \leq k \leq n$ we have $$ Q(m_k)\cdot R(m_k)=-1. $$

  This implies that either $Q(m_k)=1, R(m_k)=-1$ or $Q(m_k)=-1, R(m_k)=1$. We therefore get $$ Q(m_k)+R(m_k)=0 \qquad \forall 1 \leq k \leq n. $$ It follows that $Q(X)+R(X)$ is a polynomial of degree at most $n-1$, which has $n$ distinct roots. Therefore $$ Q(X)+R(X) \equiv 0. $$

  This implies that $R(X)=-Q(X)$ and hence $$ P(X)=-\left( Q(X) \right)^2. $$

  But this is not possible since the leading coefficient of $P(X)$ is one. We therefore get a contradiction.

  Since we got a contradiction, our assumption that $P(X)$ is reducible is wrong, and therefore $P(X)$ is irreducible, as claimed.

Week 3

• Problem (posted September 18th)

  This week we look at areas inside a trapezoid.

  The two diagonals of a trapezoid divide it into four triangles. The areas of three of them are 1, 2 and 4 square units. What values can the area of the fourth triangle take?

• Solution (posted September 25th)

  Problem 19 of the 19^th Lithuanian Team Contest, which appeared in Crux Mathematicorum [2008:282-284]. We present the solution by George Tsapakidis which appeared at [2009:303].

  

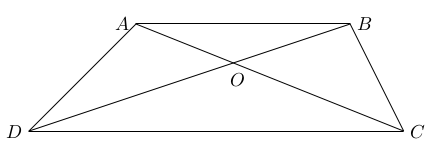
  For a triangle with vertices $X,Y$ and $Z$, we will denote by $[XYZ]$ its area.

  Since $\Delta ABD$ and $\Delta ABC$ have the same basis $AB$ and equal altitudes to this basis, they have the same area. Therefore $$[OAD]+[OAB]=[ABD]=[ABC]=[OBC]+[OAB].$$

  Therefore, $[OAD]=[OBC]$.

  Next, since the altitude from $B$ to the sides $AO, OC$ is the same, we have $$\frac{[AOB]}{[BOC]}=\frac{AO}{CO}.$$

  Same way, since the altitude from $D$ to the sides $AO, OC$ is the same, we have $$\frac{[DOA]}{[DOC]}=\frac{AO}{CO}.$$

  Therefore, $$[DOA]\cdot [BOC] = [DOC] \cdot [AOB].$$

  Since $[AOD]=[BOC]$ and three of the areas are $1,2,4$ it follows that $$[AOD]=[BOC] =2$$ that is, the fourth triangle has an area of $2$ square units.

Week 2

• Problem (posted September 11th)

  This week we look at a problem involving colourings of the positive integers.

  Each positive integer is colored either red or green, so that the following three conditions hold:

  1. The sum of any three (not necessarily distinct) red numbers is red.
  2. The sum of any three (not necessarily distinct) green numbers is green.
  3. There is at least one red and one green number.

  Find all possible such colorings.

• Solution (posted September 18th)

  Problem 2 of the Bundeswettbewerb Mathematik 2007, which appeared in Crux Mathematicorum [2010:22]. We present the solution by Titu Zvonaru which appeared at [2011:31].

  Let $R$ be the set of all red numbers and $G$ the set of all green numbers.

  First let us prove by induction that if $a \in R$ and $n$ is a non-negative integer, then $(2n+1) \cdot a \in R$. Indeed, the initial step $P(0): (2 \cdot 0+1)\cdot a \in R$   is by assumption, and the inductive step is immediate: $$(2(n+1)+1)\cdot a =((2n+1)\cdot a)+a+a$$ is the sum of three elements in $R$ and therefore, belongs to $R$.

  Same way, we can prove by induction that if $b \in G$ and $n$ is a non-negative integer, then $(2n+1)\cdot b \in G$.

  We know by (iii) that there exists some numbers $a \in R, b\in G$. Therefore, by the above, $R$ and $G$ are infinite.

  We know that $1 \in R$ or $1 \in G$. It is enough to study the case $1 \in R$, as the other case follows by flipping the colours.

  So, for the rest of the proof we will assume that $1 \in R$. We show that $R$ is the set of all positive odd integers, and hence, it will follow that $G$ is the set of all positive even integers.

  Indeed, since $1 \in R$, by the above $(2k+1)\cdot 1 \in R$ and hence $R$ contains all the odd positive integers.

  Assume next by contradiction that $R$ contains an even integer $2m$. Then, for all $n >m$ we have $$2n=2m+(2(n-m-1)+1)+1 \in R.$$

  Therefore, $R$ contains all odd integers, and all even integers larger than $2m$. But this contradicts the fact that $G$ is infinite.

  Since we got a contradiction, our assumption that $R$ contains an even integer is wrong.

  It follows that $R$ consists of all positive odd integers, and $G$ consists of all positive even integers.

  Answer: There are exactly two such colorings:

  • All positive odd integers are green and all positive even integers are red.
  • All positive odd integers are red and all positive even integers are green.

Week 1

• Problem (posted September 4th)

  We give two entry level problems this week. Give them a try. Look for the source and the solution next week!

  Problem A
  Find the sum of all positive integers $n$, such that $2009+n^2$ is the square of a positive integer.

  Problem B
  The diagram shows three squares. Find the measure of the angle $\alpha +\beta$.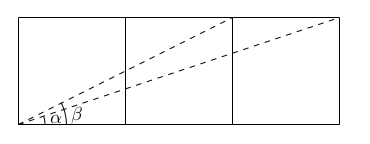

  

• Solution (posted September 11th)

  Problem A

  Problem 8 of the Niels Henrik Abel Mathematical Contest 2008- 2009, which appeared in the Skoliad Corner of Crux Mathematicorum [2009:481-483]. We present the solution by Lena Choi that appeared at [2010: 358].

  If $$n^2+2009=x^2$$ then $$x^2-n^2=(x-n)(x+n)=2009.$$

  Since $2009=41 \cdot 7^2$, $2009$ can be written as a product of two positive integers in only three ways:

  $2009=1$ · $2009$

  $2009=7$ · $287$

  $2009=41$ · $49.$

  Since $x,n$ are both positive, $x+n >x-n$. Therefore we have the solutions

  $x+n = 2009$	$x-n= 1$	⇒ $n=1004$
  $x+n = 287$	$x-n= 7$	⇒ $n=140$
  $x+n = 49$	$x-n= 41$	⇒ $n=4$.

  Therefore, their sum is $$1004+140+4=1148.$$

  Problem B

  Problem 5 of the 2005 BC Colleges High School Mathematics High School Contest, Junior Final Round B, which appeared in the Skoliad Corner of Crux Mathematicorum [2004:385-387]. We present the solution by Alex Wise, and a slight modification of the official solution that appeared at [2005: 135].

  First Solution

  We have $\tan(\alpha)=\frac{1}{3}$ and $\tan(\beta)=\frac{1}{2}$. Therefore $$\tan(\alpha+\beta)= \frac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}=\frac{\frac{1}{3}+\frac{1}{2}}{1-\frac{1}{6}}=1.$$

  Since $\alpha, \beta$ are acute, we have $0 < \alpha +\beta <180^\circ$ and hence $\alpha+\beta=45^\circ$.

  Second Solution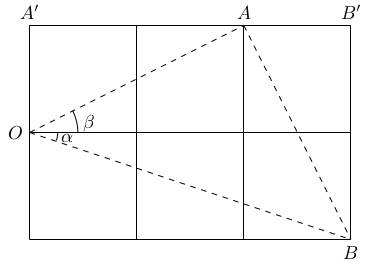

  

  If we flip the squares as shown in the diagram above, we have $\Delta OA'A \equiv \Delta AB'B$, and hence

  $OA$	$=$	$AB$
  $\angle OAA'+ \angle BAB'$	$=$	$\angle OAA'+\angle AOA'=90^\circ.$

  Therefore, $\Delta OAA'$ is an isosceles right triangle and hence $$\alpha+\beta =45^\circ.$$