Week 9

• Problem (posted November 1st)

  Find all polynomials $f(x)=x^n+a_{1}x^{n-1}+a_2x^{n-2}+...+a_{n-1}x+a_n$ with the following properties:

  1. all the coefficients $a_1,..,a_{n}$ belong to the set $\{ -1,1\}$;
  2. all the roots of the equation $f(x)=0$ are real.

• Solution (posted November 8th)

  This was Problem 5 of the Fourth Irish Mathematical Olympiad, 1991, which appeared in Crux Mathematicorum [1993:192-193]. We present the solution by Michael Selby which appeared at [1995:12-13].

  Let $r_1,r_2,..,r_n$ represent the roots of this polynomial. Then \begin{align} r_1+r_2+...+r_n &= -a_{1} \cr r_1r_2+r_1r_3+...+r_{n-1}r_n &= a_{2} \cr r_1r_2...r_n &= (-1)^na_n \,. \end{align}

  We therefore get \begin{align} r_1^2+r_2^2+..+r_n^2 &= \left(r_1+...+r_n\right)^2-2 \left(r_1r_2+r_1r_3+...+r_{n-1}r_n \right) \cr &= 1-2a_{2} \,. \end{align}

  This implies that, as long as $n \geq 2$, we have $1-2a_2 \geq 0$ and hence $a_2=-1$.

  Next, by the Arithmetic Mean-Geometric Mean inequality we get \begin{align} \frac{r_1^2+...+r_n^2}{n} &\geq \sqrt[n]{r_1^2r_2^2...r_n^2} \cr &= \sqrt[n]{ \left( (-1)^na_n \right)^2}=1 \end{align} with equality if and only if $r_1^2=r_2^2=...=r_n^2=1$.

  Therefore \[ 1-2a_2 \geq n \,, \] with equality if and only if $r_1^2=r_2^2=...=r_n^2=1$.

  Therefore $n \leq 3$.

  Case 1: $n=1$. It is straightforward to see that in this case both $X+1$ and $X-1$ work.

  Case 2: $n=2$. Then we must have $a_2=-1$, therefore, the possible polynomials are $X^2-X-1$ and $X^2+X-1$, and both work.

  Case 3: $n=3$. Then we have $a_2=-1$ and equality in the AM-GM inequality, hence $r_j \in \{ \pm 1 \}$. Moreover, since $r_1r_2+r_1r_3+r_2r_3=-1$, it is not possible for all three roots to have the same sign. This leaves us with two possible polynomials: \begin{align} (X-1)^2(X+1) &= X^3-X^2-X+1 \cr (X-1)(X+1)^2 &= X^3+X^2-X-1 \cr \end{align}

  Answer: There are 6 such polynomials: \[ X-1 \,;\, X+1 \,;\, X^2-X-1 \,;\, X^2+X-1 \,;\, X^3-X^2-X+1 \mbox{ and } X^3+X^2-X-1 \,. \]

Week 8

• Problem (posted October 25th)

  We cut an equilateral triangle $AXY$ from the rectangle $ABCD$ in such a way that the vertex $X$ is on side $BC$ and that vertex $Y$ is on side $CD$. Prove that among the remaining three right triangles there are two, the sum of whose areas equals the area of the third.

  

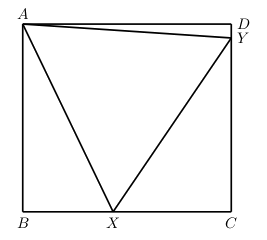
• Solution (posted November 1st)

  This was Problem 2 of the Hungarian National Olympiad, 1987, which appeared in Crux Mathematicorum [1989:100-101]. We present the solution by Michael Selby and D.J. Smeenk which appeared at [1991:68-69].

  First, this is not possible in every rectangle. If the rectangle has sides $a \leq b$, then a necessary condition is that $a \geq \frac{\sqrt{3}}{2}b$.

  Now, if we can cut such a triange, let $s$ denote the side of the triangle. We claim that \[ [XYC]=[ADY]+[ABX] \,, \] where $[T]$ denotes the area of the triangle $T$. Let us denote by $\theta_1$ and $\theta_2$, respectively the angles $\angle BAX$ and $\angle DAY$, respectively.

  

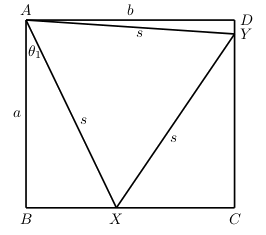
  Then \begin{align} [ABX] &= \frac{1}{2} AB \cdot BX \cr &= \frac{1}{2} s \cos(\theta_1) s \sin(\theta_1) \cr &= \frac{1}{2} s^2 \cos(\theta_1) \sin(\theta_1) \cr &= \frac{1}{4} s^2 \sin(2 \theta_1) \,, \end{align} and same way \[ [ADY] =\frac{1}{4} s^2 \sin(2 \theta_2) \,. \]

  Therefore \begin{align} [ADY] &= \frac{1}{4} s^2 \sin(2 \theta_2) \cr &= \frac{1}{4} s^2 \sin\left(2 (30^\circ -\theta_1)\right) \cr &= \frac{1}{4} s^2 \sin\left(60^\circ -2\theta_1\right) \cr &= \frac{1}{4} s^2 \left( \frac{\sqrt{3}}{2} \cos(2\theta_1) -\frac{1}{2} \sin(2\theta_1) \right) \cr &= \left(\frac{\sqrt{3}}{8} s^2 \cos(2\theta_1) \right) -\left( \frac{1}{8} s^2 \sin(2\theta_1) \right) \,. \end{align}

  This shows that \[ [ADY]+[ABX]= \frac{\sqrt{3}}{8} s^2 \cos(2\theta_1) +\frac{1}{8} s^2 \sin(2\theta_1) \,. \]

  Now, for $XCY$ the angle $\angle CXY= 30^\circ+\theta_1$. Therefore \begin{align} [CXY] &= \frac{1}{2} CX \cdot CY \cr &= \frac{1}{2} s^2 \sin(30^\circ+\theta_1) \cos(30^\circ+\theta_1) \cr &= \frac{1}{4} s^2 \sin(60^\circ+2 \theta_1) \cr &= \frac{\sqrt{3}}{8} s^2 \cos(2\theta_1) +\frac{1}{8} s^2 \sin(2\theta_1) \cr &= [ADY]+[ABX] \,. \end{align}

Week 7

• Problem (posted October 18th)

  $ABC$ is a triangle with $AB=AC$ and $\angle BAC=20^\circ$. On the side $AC$ we pick inside a point $D$ such that $AD=BC$. Find the measure of the angle $\angle CDB$.

  

• Solution (posted October 25th)

  This is one of my favourite geometry problems, with a very nice solution. Unfortunately we lost the source of this problem and of the solution below.

  On side $AD$ we construct outside an equilateral triangle $ADE$. Connect $E$ to $B$.

  

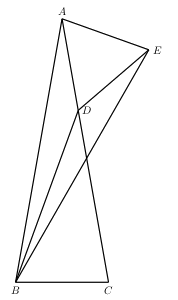
  Now, by SAS, triangles $ABC$ and $BAE$ are congruent. Indeed \[ AB=AC \,;\, \angle ABC=80^\circ =\angle BAE \,;\, BC=AE \,. \]

  Then, it follows that triangle $BAE$ is isosceles and hence $AB=BE$.

  Then, by SSS, triangles $ADB$ and $EDB$ are congruent. Indeed \[ AD=ED \,;\, DB=DB \,;\, AB=EB \,. \] It follows that $\angle ADB=\angle EDB$.

  Since \[ \angle ADB+\angle EDB+60^\circ =360^\circ \] we get \[ \angle ADB =150^\circ \,. \] Then \[ \angle CDB =30^\circ \,. \]

Week 6

• Problem (posted October 11th)

  Find all the natural numbers $n$ such that the number \[ n(n+1)(n+2)(n+3) \] has exactly 3 prime divisors.

• Solution (posted October 18th)

  Problem 5 of the 30^th Spanish Mathematical Olympiad, Final Round, 1993, which appeared in Crux Mathematicorum [1998:69-70]. We present the solution by Edward T.H. Wang which appeared at [1999:203-204], slightly modified.

  We prove that the only such integers are $n=2,3$ and $6$.

  Let $P(n)=n(n+1)(n+2)(n+3)$. Then $P(1)=2^3 \cdot 3$ and thus $n=1$ is not a solution. Hence we assume $n \geq 2$.

  Note first that for all $k \in \mathbb{N}$ we have $(k,k+1)=(2k-1,2k+1)=1$.

  We have two cases:

  Case 1: $n$ is odd. Then the numbers $n, n+1, n+2$ are by the above pairwise relatively prime, and hence each needs to be a power of a prime.

  Since $n+1$ is even, we must have \[ n=p^a \,;\, n+1=2^b \, \mbox{ and } \, n+2=q^c \] where $a, b, c, p, q \in \mathbb N$ with $p,q$ distinct odd primes.

  Note now that $n+3=2^{b}+2=2(2^{b-1}+1)$ where $b \geq 2$. Since the only possible prime divisors of $n+3$ are $2, p$ and $q$ and $(n+2,n+3)=1$ we must have \[ 2^{b-1}+1=p^d \,, \] with $d \geq 1$.

  Therefore, \[ 2p^d=n+3=p^a+3 \,. \]

  This shows that $p|3$ and hence $p=3$. Dividing by $3$, we get \[ 2 \cdot 3^{d-1}=3^{a-1}+1 \,. \]

  Now, we cannot have $d-1>0$ and $a-1>0$, as in this case we would get $3|1$. Therefore one of $d-1$ or $a-1$ must be $0$, and it is immediate that the other one is also zero.

  This shows that $a=1$, and hence $n=3$.

  We showed that the only possible solution with $n$ odd is $n=3$, and it is easy to check that this is indeed a solution.

  Case 2: $n$ is even. Then, we have $(n+1,n+2)=(n+1,n+3)=(n+2,n+3)=1$. By the same argument as in Case 1 we must have \[ n+1=p^a \,;\, n+2=2^b \, \mbox{ and } \, n+3=q^c \] where $a, b, c, p, q \in \mathbb N$ with $p,q$ distinct odd primes.

  Now, \[ n=2^b-2=2(2^{b-1}-1) \,. \]

  We know that $n\geq 2$ and hence $b \geq 2$.

  If $b=2$ we get $n=2$ which is a solution.

  Otherwise $b \geq 3$ and hence $2^{b-1}-1$ is an odd number greater or equal than $3$. The only primes which can divide $n$ are $2,p,q$ and as $(n, p^a)=1$ and $2^{b-1}-1$ is odd, we must have \[ 2^{b-1}-1=q^d \,, \] with $d \geq 1$.

  Therefore, \[ 2q^d=n=q^c-3 \,. \] This shows that $q|3$ and hence $q=3$. Dividing by $3$, we get \[ 2 \cdot 3^{d-1}=3^{c-1}-1 \,. \] We must have $d-1 \leq c-1$ and hence $3^{d-1} |1$. This shows that $d=1$ and hence \[ n=2 \cdot 3=6 \,. \]

  It is easy to check that $n=6$ is indeed a solution.

  In conclusion, $n(n+1)(n+2)(n+3)$ has exactly three prime divisors if and only if $n \in \{2,3,6\}$.

Week 5

• Problem (posted October 4th)

  This week we look at a functional equation.

  Find all functions $f : \mathbb{N}^* \to \mathbb{N}^*$ such that \[ f\left(f(m)+f(n) \right) = m+n \,;\, \forall m,n \in \mathbb{N}^* \,, \] where $\mathbb{N}^*$ denotes the set $\{1,2,3,...\}$ of positive integers.

• Solution (posted October 11th)

  Problem 4 of the 44^th Lithuanian Mathematical Olympiad, which appeared in Crux Mathematicorum [1998:196-197]. We present the solution by Pierre Bornsztein which appeared at [1999:334-335].

  For all $m,n \in \mathbb{N}^*$, we have \[ f\left(f(m)+f(n) \right) = m+n \tag{1} \] \[ f\left(f(m)+f(n) \right)+f\left(f(m)+f(n) \right) =2( m+n) \,. \]

  Therefore \begin{align} f\left[ f\left( f(m)+f(n) \right)+f\left(f(m)+f(n) \right) \right] & = f(m)+f(n)+f(m)+f(n) \cr & = 2\left( f(m)+f(n) \right) \end{align} and \[ f\left[ f\left(f(m)+f(n) \right)+f\left(f(m)+f(n) \right) \right] = f(2m+2n) \,. \]

  It follows that \[ f(2m+2n)=2\left( f(m)+f(n) \right) \,. \tag{2} \]

  Setting $m=n$, we get $4f(n)=f(4n)$.

  Setting $m=2p+1, n=2p-1$ we also get \[ 2f(2p+1)+2f(2p-1)=f(8p)=4f(2p) \] for all $p \geq 1$, and hence \[ f(2p+1)=2f(2p)-f(2p-1) \,. \tag{3} \]

  Setting $m=2p+2, n=2p-2, (p \geq 2)$ we get \[ f(2p+2)=2f(2p)-f(2p-2) \,. \tag{4} \]

  Let us set $f(1)=a, f(2)=b$.

  Using $(3)$ and $(4)$ we get \begin{align} f(3) &= 2b-a \cr f(4) &= f(4 \cdot 1)=4f(1)=4a \cr f(5) &= 9a-2b \cr f(6) &= 8a-b \end{align}

  Now, using $m=2,n=1$ in $(2)$ we get \[ f(6)=2f(2)+2f(1)=2a+2b \,. \]

  Thus $8a-b=2a+2b,$ hence $b=2a$. It follows that for $n \in \{ 1, 2, 3, 4, 5, 6 \}$ we have \[ f(n)=an \,. \]

  Now, using $(3)$ and $(4)$ by induction we get immediately \[ f(n)=an, \, \mbox{ for all } n \in \mathbb{N}^*. \]

  Now, by $(1)$, for all $m,n \in \mathbb{N}^*$ we have \[ m+n=f\left(f(m)+f(n) \right)=a(f(m)+f(n))=a^2(m+n) \,. \]

  Therefore $a=1$ and \[ f(n)=n \, \mbox{ for all } n \in \mathbb{N}^* \,. \]

  Conversely, $f(n)=n$ works.

Week 4

• Problem (posted September 27th)

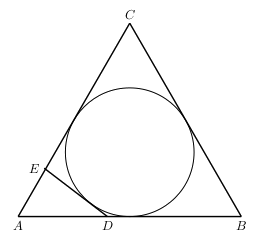
  This week we will look at an inscribed circle problem.

  Let $ABC$ be an equilateral triangle and $\Gamma$ its incircle. If $D$ and $E$ are points on the sides $AB$ and $AC$, respectively, such that $DE$ is tangent to $\Gamma$, show that \[ \frac{AD}{DB}+\frac{AE}{EC}=1 \]

  

• Solution (posted October 4th)

  Problem 4 of of the 8^th IberoAmerican Mathematical Olympiad 1993, which appeared in Crux Mathematicorum [1996:159-160]. We present the solution by Sěfket Arslanagić which appeared at [1997:465-466].

  Let $AB=AC=BC=a, BD=p$ and $CE=q$. Then $AD=a-p$ and $AE=a-q$.

  

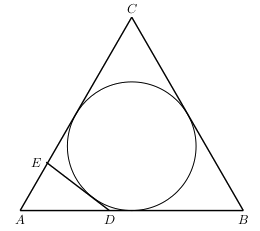
  Since the circle $\Gamma$ is inscribed in the quadrilateral $BCED$ we have \[ ED+BC=BD+CE \,, \] or \[ED=p+q-a \,.\tag{1}\]

  By the Law of cosines in the triangle $ADE$ we get \[ ED^2=AD^2+AE^2-2AD \cdot AE \cdot \cos(60^\circ) \,, \] and hence, by $(1)$ \[ (p+q-a)^2=(a-p)^2+(a-q)^2-(a-p)(a-q) \,. \] This gives \[ 3pq=ap+aq\,. \]

  Then \begin{align} \frac{AD}{DB}+\frac{AE}{EC} & = \frac{a-p}{p}+\frac{a-q}{q} \cr & = \frac{aq-pq+ap-qp}{pq} \cr & = \frac{ap+aq-2pq}{pq} \cr & = 1 \,. \end{align}

Week 3

• Problem (posted September 20th)

  Let $p$ be the number of functions defined on the set $\{ 1, 2, 3, ..., m \}$, $m \in \mathbb{N}^{*}$, with values in the set $\{1, 2, ..., 35, 36\}$ and $q$ be the number of functions defined on the set $\{ 1, 2, 3, ..., n \}$, $n \in \mathbb{N}^{*}$, with values in the set $\{1, 2, 3, 4, 5\}$. Find the least possible value for the expression $|p-q|$.

• Solution (posted September 27th)

  Problem 5 of the Republic of Moldova XL Mathematical Olympiad, form 11, which appeared in Crux Mathematicorum [1999:326-327]. We present the solution by Pierre Bornsztein which appeared at [2001:369-370], slightly modified.

  Let $m,n \in \mathbb{N}^{*}$. We have $p=36^m$ and $q=5^n$. The problem is then to find the least possible value of $|36^m-5^n|$ over all $m,n \in \mathbb{N}^{*}$.

  The last two digits of $36^m$ can be $36, 96, 56, 16$ or $76$. The last two digits of $5^n$ are either $5$ or $25$.

  This shows that \[ 36^m-5^n \in \{ \pm 9, \pm 11, \pm 29, \pm 31, \pm 49 \} \pmod{100} \]

  Let us also observe that since $9|36^m$ and $9 \nmid 5^n$ we have $9 \nmid 36^m-5m$. Therefore $36^m-5^n \neq \pm 9$.

  This shows that the smallest possible value $|36^m-5^n|$ could take is $11$. This value is achieved when $m=n=2$.

  Therefore, the least possible value of $|p-q|$ is 11.

Week 2

• Problem (posted September 13th)

  This week we look at a Quintic Equation.

  Find all real solutions to the equation \[ 1+x+x^2+x^3=x^4+x^5 \,. \]

• Solution (posted September 20th)

  Problem 4 of the $21^{st}$ W.J. Blundon Mathematics Contest, Memorial University which was written in February 2004 and given in the Skoliad Corner of Crux Mathematicorum in [2005:354].

  The equation can be written as \[ (1+x)(1+x^2)=(1+x)x^4 \,. \]

  It is clear that $x=-1$ is a solution.

  If $x \neq -1$ we can divide by $1+x$ to get \[ 1+x^2=x^4 \,, \] or \[ x^4-x^2-1=0 \,. \]

  Substituting $y=x^2$ we get the quadratic equation \[ y^2-y-1=0 \] with solutions \[ y_1= \frac{1+\sqrt{5}}{2} \mbox{ and } y_2= \frac{1-\sqrt{5}}{2} \,. \]

  Since $y_2 <0$ the equation $x^2=y_2$ has no solution.

  Solving $x^2=y_1$ we get two more real solutions \[ x= \pm \sqrt{\frac{1+\sqrt{5}}{2}} \,. \]

  Therefore, the equation has $3$ real solutions: \[ x=-1, x=\sqrt{\frac{1+\sqrt{5}}{2}} \mbox{ and } x=-\sqrt{\frac{1+\sqrt{5}}{2}} \,. \]

Week 1

• Problem (posted September 6th)

  We give two entry level problems this week. Give them a try. Look for the source and the solution next week!

  Problem A
  In the diagram, $ABCD$ is a square with side length 17 and the four triangles $ABF, DAE, BCG$, and $CDH$ are congruent right triangles. Furthermore, $\overline{FB}=8$. Find the area of the shaded quadrilateral $EFGH$.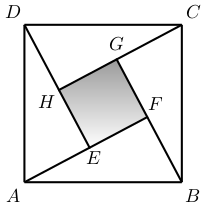

  

  Problem B
  Find the number of solutions in integers $(x,y)$ of the equation \[ x^2y^3=6^{12} \,. \]

• Solution (posted September 13th)

  Problem A

  This was Problem 1 of BC Colleges High School Mathematics Contest 2005, Junior Final Round B, written in May 2005, and given in the Skoliad Corner of Crux Mathematicorum in [2005:265]. We give the "official" solution which appeared at [2006:137].

  Since $FB=8$ and $AB=17$, the Pythagorean Theorem gives $AF=15$. The area of each of the four congruent triangles is $\frac{8 \times 15}{2}=60$. Thus the area of the shaded square $EFGH$ is $17^2-4\cdot 60=49$.

  Problem B

  This was Problem 3 of the same contest. We give the "official" solution which appeared at [2006:138].

  First, since $6^{12} >0$ and $x^2 \geq 0$ we must have $x^2 >0$ and $y>0$.

  We are given that $x^2y^3=6^{12}=2^{12}3^{12}$. Since $x$ and $y$ both divide $2^{12}3^{12}$ we must have $x= \pm 2^i3^j$ and $y= 2^k3^l$, where $i,j,k $ and $l$ are non-negative integers.

  Then $x^2=2^{2i}3^{2j}$ and $y^3=2^{3k}3^{3l}$. Therefore \[x^2y^3=2^{2i+3k}3^{2j+3l} \,.\]

  We want $x^2y^3=2^{12}3^{12}$. Thus $2i+3k=12$ and $2j+3l=12$. Solving these equations we get \[ (i,k) \in \{ (0,4), (3,2), (6,0) \} \mbox{ and } (j,l) \in \{ (0,4), (3,2), (6,0) \} \,. \]

  Now, each of the three values of $i$ can be paired with each of the three values of $j$. Once this is done, the values of $k$ and $l$ are determined. Therefore, the number of solutions in positive integers is $3 \times 3=9$, and the the total number of solutions is $9 \times 2=18$.