Week 9

• Problem (posted October 27th)

  Define the function $t(n)$ on the nonnegative integers by $t(0) = t(1) = 0$, $t(2) = 1$, and for $n>2$ let $t(n)$ be the smallest positive integer which does not divide $n$. Let $T(n) = t(t(t(n))).$ Find the value of $S$ if $$ S = T(1) + T(2) + T(3) + \cdots + T(2006).$$

• Solution (posted November 3rd)

  This was problem 1 of the Final Round of the Hungarian Mathematical Olympiad 2005-2006 National Olympiad, Grades 11-12 given in the Olympiad Corner of Crux Mathematicorum at [2009:211-212]. The solution given was a modification of the solution by Michel Bataille, Rouen, France, given at [2010:281]

  We observe that $T(n) = 0$ if $n = 2$ or if $n$ is an odd integer, hence
  $S = T(4) + T(6) + \cdots +T(2006).$

  If $n \in \mathbb{P} = \{4,6,8, \cdots, 2006\}$ and $n$ is not a multiple of $3$, then $t(n) =3$ and $T(n) =1.$

  Let $\mathbb{P}_1 = \{6, 18,30, \cdots ,6 \cdot 333 \}$ be the set of elements of $\mathbb{P}$ of the form $6(2m-1),$ and let $\mathbb{P}_2$ be the set of elements of $\mathbb{P}$ of the form $12m$.

  For each $n \in \mathbb{P}_1,$ we have that $t(n)=4,$ hence $T(n) = 2$, and there are $167 $ numbers in $\mathbb{P}_1.$

  If $n \in \mathbb{P}_2$ and $n$ is not a multiple of $5$ or $n$ is not a multiple of $7$ , then $t(n) = 5 $ or $t(n) = 7$ and then $T(n) =1$. Otherwise $T(n)$ is one of the following: $T(420) = 2, T(840)=1, T(1260) = 2,$ or $T(1680) = 1$.

  Thus $T(n)=1$ for each $n \in \mathbb{P}_2$, except for two numbers where $T$ takes the value $2$.

  In summary $T(n) = 2 $ for $167+2=169 $ numbers and $T(n)=1 $ for the $1002-169 = 833$ remaining numbers. Therefore, $S = 833+2 \cdot 169 = 1171.$

Week 8

• Problem (posted October 20th)

  Let $A$ be a fixed exterior point with respect to a given circle with centre $O$ and radius $r$. Let $M$ be a point on the circle, and let $N$ be diametrically opposite to $M$ with respect to $O$. Find the locus of the centres of the circles passing through $A,M,$ and $N$, as the point $M$ is varied on the circle.

• Solution (posted October 27th)

  This was problem 2 of the XIX Olimpiada Iberoamericana de Matematicas, that was given in the Olympiad Corner of Crux Mathematicorum at [2008:14]. The solution, by Michel Bataille, of Rouen, France was given at [2009:219].

  Let $U$ be the circumcentre of $\triangle AMN$. Since $O$ is the midpoint of $MN,\ UO$ is orthogonal to $MN$ and $UM^2 = UO^2 +r^2.$

  

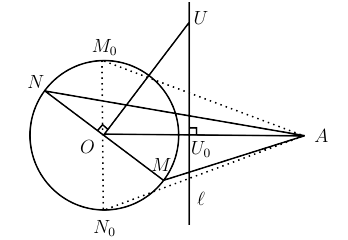
  But $UM = UA$, so we have $UA^2-UO^2=r^2.$ It follows that $U$ is on a line ${\it l}$ perpendicular to $AO$. More precisely, if $M_0N_0$ is the diameter perpendicular to $AO$ and $U_0$ is the circumcentre of $\triangle AM_0N_0$, then ${\it l}$ is the perpendicular to $AO$ through $U_0$. Note that $U_0 \neq O$.

  Conversely, let $U$ be any point on ${\it }$ (so that $UA^2 -UO^2 = r^2)$, and let $MN$ be the diameter perpendicular to $UO$. Then $UO^2+r^2 = UM^2=UN^2$ so that $UM=UN=UA$ and $U$ is the circumcentre of $\triangle AMN $ (note that $A,M,$ and $N$ are not collinear because $U_0 \neq O)$.

Week 7

• Problem (posted October 13th)

  Find the positive values of $x$ that satisfy $$ x^{(2 \sin x - \cos 2x )} < \frac{1}{x}.$$

• Solution (posted October 20th)

  This was problem 1 of the National Olympiad, Grades 11-12 of the Hungarian Mathematical Olympiad 2005-2006. It was given in the Olympiad Corner of Crux Mathematicorum at [2009:211]. The solution, by Oliver Geupel, Brühl, NRW, Germany, was given at [2010:280].

  Since $\cos 2x = 1 - 2 \sin^2 x$ and $x >0$, the given inequality is equivalent to $x^{2 \sin x (1+ \sin x)} <1.$ Write $a = 2 \sin x (1+\sin x).$ For $x >0,$ the inequality $x^a <1$ holds if and only if either
  (1) $ 0 < x < 1$ and $a>0$, or
  (2) $x>1$ and $a<0.$

  If $0 < x < 1$, then we have $\sin x >0$, hence the condition (1) is satisfied.

  If $x >1$, then $a < 0$ holds if and only if $-1 < \sin x < 0.$ Thus, (2) is equivalent to $(2k+1) \pi < x < (2k + \frac{3}{2}) \pi$ or $(2k+\frac{3}{2}) \pi < x < (2k+2)\pi$ for some non-negative integer $k$. Consequently, the solution set is the union of these open intervals. $$(0,1) \cup \bigcup_{k=0}^\infty \left( (2k+1 )\pi,\left(2k+\frac{3}{2}\right) \pi \right) \cup \bigcup_{k=0}^\infty \left( \left( 2k+\frac{3}{2} \right) \pi,(2k+2)\pi\right)$$

Week 6

• Problem (posted October 6th)

  Let $f:[0,4] \rightarrow [0,\infty)$, be such that $f(4) =2$ and $f(x+y) \geq f(x) + f(y)$ for any real numbers $x$ and $y$ in the closed interval $[0,4]$ such that $x+y \leq 4.$

  (a) Suppose that $0 \leq x \leq y \leq 4.$ Show that $f(y) \geq f(x).$

  (b) Show that $f(x) \leq x$ for any $x$ in $[0,4].$

• Solution (posted October 13th)

  This was Problem 3 of the the 2014-2015 ConocoPhillips Alberta High School Mathematics Prize Examination, which was written in February, 2015.

  (a) If $0 \leq x \leq y \leq 4$ then $f(y) = f(x+(y-x)) \geq f(x) + f(y-x) \geq f(x)$.

  (b) If $x$ is in $[2,4]$, then $f(x) \leq f(4) = 2 \leq x$. On the other hand, if $x$ is in $(0,2)$, then $\frac{4}{x} - \frac{2}{x} = \frac{2}{x} >1.$ Hence there is a positive integer $n$ such that $\frac{2}{x} < n < \frac{4}{x}$ or $2 < n x < 4,$ so that $f(n x) \leq n x$. Also, $f(n x) = f((n-1)x+x) \geq f((n-1)x)+f(x) \geq f((n-2)x)+2f(x) \geq \cdots \geq n f(x)$ and hence $f(n x) \geq n f(x).$ Consequently $n f(x) \leq f(n x) \leq n x$, that is, $f(x) \leq x$ for any $x $ in $(0,2)$. Therefore $f(x) \leq x$ for any $x$ in $[0,4]$.

Week 5

• Problem (posted September 29th)

  Time for some more geometry.

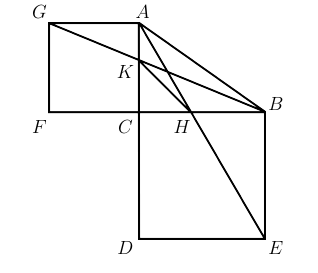
  Let $ABC$ be a right-angled triangle with the right angle at $C$. Let $BCDE$ and $ACFG$ be squares external to the triangle. Furthermore, let $AE$ intersect $BC$ at $H$, and let $BG$ intersect $AC$ at $K$. Find the size of $\angle DKH$.

  

• Solution (posted October 6th)

  This was problem 1 of the 2005 Australian Mathematical Olympiad given in the Olympiad Corner of Crux Mathematicorum at [2009:146-147]. The solution by Geoffrey Kandall, Hamden Connecticut, USA, was given at [2010:229].

  Let $BC = a$ and $AC = b$. Triangle $KCB$ is similar to triangle $GFB$ and triangle $HCA$ is similar to triangle $EDA$. Therefore,
  $\frac{KC}{b} = \frac{a}{a+b}$ and $\frac{HC}{a} = \frac{b}{a+b}.$

  Consequently, $KC = HC = \frac{ab}{a+b}$ Hence $\angle DKH = 45^\circ$.

Week 4

• Problem (posted September 22nd)

  Determine all pairs of real numbers $(x,y)$ such that $$x^6 = y^4 +18,$$ $$y^6 =x^4 + 18.$$

• Solution (posted September 29th)

  This was problem 6 of the Lithuanian Team Contest 2004 given in the Olympiad Corner of Crux Mathematicorum at [2008:282-284]. The solution given at [2009:298] was by George Apostolopoulos, Messolnghi, Greece.

  Observe that $x \neq 0$ and $y \neq 0$. Since $x^6-y^4 = 18$ and $y^6-x^4 =18$ we have

  $\begin{array}{ccc} x^6-y^6 +x^4-y^4 &=& 0 \\(x^2)^3-(y^2)^3 +(x^2)^2 -(y^2)^2 & = & 0 \\(x^2-y^2)(x^4 +x^2y^2 +y^4) + (x^2-y^2)(x^2+y^2) & = & 0\\(x^2-y^2)(x^4+x^2y^2+y^4+x^2+y^2) & = & 0 \end{array}$

  However, $x^4+x^2y^2+y^4+x^2+y^2>0,$ hence $x^2=y^2$ and $x^6-x^4-18=0$. We put $x^2 =w$, then the equation in $x$ becomes $w^3-w^2-18=0$, or $(w-3)(w^2+2w+6)=0$, hence $w=3$, since $w^2+2w+6 = x^4+2x^2+6$ is positive for all real numbers. Now $x^2=w = 3$, hence $x= \pm \sqrt{3}$ and there are four solutions $(x,y) = (\pm \sqrt{3},\pm \sqrt{3}).$

Week 3

• Problem (posted September 15th)

  Let $a$,$b$, and $c$ be given nonzero real numbers. Find $x$, $y$ and $z$ if $$ \frac{ay+bx}{x y}=\frac{b z+c y}{y z}=\frac{c x+a z}{z x}=\frac{4a^2+4b^2+4c^2}{x^2+y^2+z^2}.$$

• Solution (posted September 22nd)

  This was Problem 3 of the Croation Mathematics Contest 2007 given in the Skoliad Corner of Crux Mathematicorum at [2008:195-196]. The solution, by Johan Gunardi, student SMPK 4 BPK PENABUR, Jakarta, Indonesia, appeared at [2009:132].

  We have that $\frac{a}{x}+\frac{b}{y} = \frac{b}{y}+\frac{c}{z} = \frac{c}{z} + \frac{a}{x}$, which implies that $\frac{a}{x}=\frac{b}{y}=\frac{c}{z}.$ Let $k$ be this common value. Then $a=k x,b=k y,$ and $c=k z$. Substituting into the given equation yields that $2k =\frac{4k^2x^2+4k^2y^2+4k^2z^2}{x^2+y^2+z^2}=4k^2$ hence $k=0$ or $k= \frac{1}{2}.$ If $k=0$, then $a=b=c=0$, contradicting the requirement that $a,b,$ and $c$ are nonzero. If $k=\frac{1}{2}$, then $x=2a,y=2b,$ and $z=2c$.

Week 2

• Problem (posted September 8th)

  Eight balls in two urns

  We give you two similar urns, four white balls, and four black balls. You must separate the balls amongst the two urns (not necessarily the same number in each urn), after which both urns will be made indistinguishable. How should the balls be distributed to maximize the chances that, if you draw a ball randomly from a randomly chosen urn, you will obtain a white ball?

• Solution (posted September 15th)

  This was problem 3 of the Quebec Concours (Secondary Level) written in February 2006 and given in the Skoliad Corner of Crux Mathematicorum in [2008:67-68]. The solution is by the editor and appeared at [2009:8].

  Put $1$ white ball in one urn and all the other balls in the other urn. The probability of choosing the urn with $1$ white ball and then drawing that white ball is $\frac{1}{2}\cdot 1= \frac{1}{2}$ and the probability of choosing the other urn and then drawing a white ball from it is $\frac{1}{2}\cdot \frac{3}{3+4}=\frac{3}{14}.$ Thus, with this distribution, the overall probability of ultimately obtaining a white ball is $p =\frac{1}{2}\cdot 1 + \frac{1}{2} \cdot \frac{3}{7}= \frac{5}{7}.$

  Now let $p_1$ and $p_2$ be the probability of drawing white balls from two urns ($p_1 =1$ and $p_2 = \frac{3}{7}$ above). The overall probability of ultimately obtaining a white ball is then $p = \frac{1}{2} p_1 + \frac{1}{2} p_2 = \frac{p_1+p_2}{2}$, which is the average of the probabilities $p_1$ and $p_2$. Therefore $p>\frac{5}{7}$ implies that $p_1 > \frac{5}{7}$ or $p_2 > \frac{5}{7}.$ To make an urn with $p_1 > \frac{5}{7}$, say, we must have $(w,b) = (1,0),(2,0),(3,0) (3,1),(4,0)$ or $(4,1),$ where the urn contains $w$ white balls and $b$ black balls. These are the only distributions which could yield $p > \frac{5}{7}.$ In the case of $(w,b) = (2,0),(3,0),$ or $(4,0)$ we have $p<\frac{5}{7}$ since moving all but one white ball to the other urn increases $p_2$, but leaves $p_1 =1.$ Finally, $(w,b) = (3,1)$ or $(4,1)$ yields $p = \frac{1}{2}$ or $p = \frac{2}{5}$, each less than $\frac{5}{7}.$

  Our first distribution maximizes our chance of obtaining a white ball.

Week 1

• Problem (posted September 1st)

  We give two entry level problems this week. Give them a try. Look for the source and the solution next week!

  Problem A
  Find two factors of $2^{48}-1$ between $60$ and $70$

  Problem B
  An arbitrary point is selected inside an equilateral triangle. From this point perpendiculars are dropped to each side of the triangle. Show that the sum of the lengths of these perpendiculars is equal to the length of the altitude of the triangle.

  

• Solution (posted September 8th)

  Problem A
  This was problem 4 of the $23^{rd}$ W. J. Blundon Mathematics Contest, written in 2006. It was given in the Skoliad Corner of Crux Mathematicorum at [2007:321-322], with a solution by Ruiqi Yi, student, Stephen Leacock Collegiate Institute, Toronto that appeared at [2008:197].
  Repeatedly using the formula $x^2-y^2=(x-y)(x+y)$, we have $$2^{48}-1=(2^{24}+1)(2^{12}+1)(2^6+1)(2^6-1).$$ Since $2^{6}= 64$, two factors of $2^{48}-1$ between $60$ and $70$ are $63$ and $65$.

  Problem B
  This was problem 8 of the same contest. The official solution modified by the editor was given at [2008:198-199]
  Let $s$ be the length of the equal sides, let $h$ be the altitude, and let $x,y,$ and $z$ be the three distances from the interior point to the sides of the triangle. Then, $$\begin{array}{ccc} \mbox{Area of triangle} &= &\frac{1}{2} s x + \frac{1}{2} s y + \frac{1}{2} s z \\ & = & \frac{1}{2}s(x+y+z). \end{array}$$

  But we also have $$\mbox{Area of triangle} = \frac{1}{2} sh$$.

  Canceling $\frac{1}{2}s $ from each expression for the area, we have $x+y+z =h$.