Week 9

• Problem (posted October 29th)

  And to round out the taste of problems to interest you in the COMC here is another type of geometry problem.

  Given three straight lines in a plane, that concur at point $O$, consider the three consecutive angles between them (which, naturally, add up to $180^{\circ}$). Let $P$ be a point in the plane not on any of these lines and let $A$, $B$, $C$ be the feet of the perpendiculars drawn from $P$ to the three lines. Show that the internal angles of $\Delta ABC$ are equal to those between the given lines.

• Solution (posted November 5th)

  The problem for week 9 is from the Chilean Mathematical Olympiads 1994-1995 and the solution is in Crux Mathematicorum 29-5 pp 292. Solution by G. Kandall, USA.

  

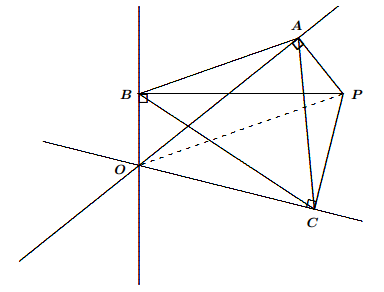
  The points $O$, $C$, $P$, $A$, $B$ lie on the circle having $\overline{OP}$ as diameter. Therefore, $\angle ABC=\angle AOC$, $\angle ACB=\angle AOB$, and, as a consequence, $\angle BAC$ is equal to the third consecutive angle at $O$.

Week 8

• Problem (posted October 22nd)

  For week 8, it is time to try some geometry.

  $ABCD$ is a quadrilateral which is circumscribed about a circle $\Gamma$ (that is, each side of the quadrilateral is tangent to $ \Gamma$). If $\angle A = \angle B = 120^\circ , \angle D = 90 ^\circ $ and $BC$ has length $1$, find, with proof, the length of $AD.$

• Solution (posted October 29th)

  The problem for week 8 is from the Tenth Irish Mathematical Olympiad with the solution given in Crux Mathematicorum 29-2 pp 99-100. Solution by M. Bataille, France.

  

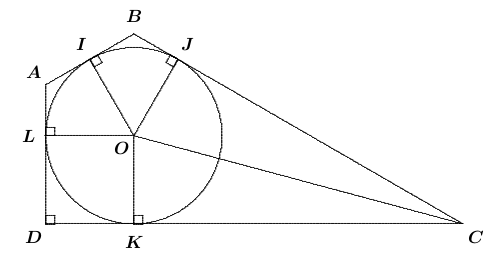
  Let $O$ be the centre of $\Gamma$, and let $I,J,K,$ and $L$ be the points at which $AB,BC,CD,$ and $DA$ touch $\Gamma $, respectively. Triangle $IBJ$ is isosceles with $\angle B = 120^\circ .$ Therefore, $\angle BIJ = \angle BJI = 30^\circ $, whence $ \angle OIJ = 60^\circ .$ It follows that $ \triangle IOJ $ is equilateral and, consequently, $ IJ = OI = OJ =R$ the radius of $\Gamma .$ Since $ \frac{\sqrt{3}}{2} = \cos 30^\circ = \frac{IJ/2}{BJ},$ we get $BJ = \frac{R}{\sqrt{3}}.$ Now, observing that $OKDL$ is a square and that $\triangle IOJ$ and $ \triangle IOL $ are equilateral triangles, we obtain $ \angle KOJ = 150^\circ .$ Then $\angle OCJ = 15^\circ ;$ whence, $2 - \sqrt{3} = \tan 15^\circ = \frac{OJ}{CJ}.$ This implies that $CJ = R(2 + \sqrt{3}).$ The relation $ 1 = BC = BJ +CJ $ now yields $ R = \frac{\sqrt{3}}{4+2\sqrt{3}} .$ Using $ DL = R$ and $AL = BJ = \frac{R}{\sqrt{3}} ,$ we can compute $AD = AL + DL = \frac{R}{\sqrt{3}} + R,$ which readily gives $ AD = \frac{\sqrt{3} -1}{2} .$

Week 7

• Problem (posted October 15th)

  For week seven we come back to questions about percent. Perhaps with a bit extra!

  From a jar of candies, Autumn takes $a$ percent of the candies plus $a$ more candies. Brooke takes $ b$ percent of the remaining candies plus $ b$ more candies. Here, $a$ and $ b$ are positive integers less than $100$. If Autumn and Brooke have taken the same number of candies, determine all possible values of $a$ and $ b.$

• Solution (posted October 22nd)

  The week 7 question is from the Alberta High School Mathematics Competition Part 2 2008. Here is the 'official' solution.

  Let the total number of candies be $n$ initially. After Autumn has taken $\frac{na}{100} + a$ candies, Brooke will take $(n- \frac{na}{100} -a) \cdot \frac{b}{100} +b$ candies. Equating these two expressions and simplifying, we obtain $na + 100 a = nb -\frac{nab}{100} - ab + 100b.$ This may be rewritten as $(n+100)(b-a-\frac{ab}{100}) = 0.$ Since $n \neq -100,$ the second factor must be zero so that $b = \frac{100a}{100-a}.$ Note that $a <50$ so that $100-a > 50.$ Let $p$ be any prime divisor of $100-a$. Then $p$ must divide $100a$ so that it divides either $100$ or $a$. It follows that $p$ must divide $100,$ so that $p$ can only be $2$ or $5$. This means that $100-a = 64$ or $80$. However $36$ does not divide $6400$. Hence $(a,b)=(20,25)$ is the only possibility. This does work if we take $n =5k$ where $3k > 40.$ Autumn will take $k+20$ candies, leaving behind $4k - 20$. Then Brooke will take $(k-5) +25 = k +20$ candies.

Week 6

• Problem (posted October 8th)

  For week six we have a type of question called a 'functional equation'.

  Determine all functions $f$ from the set of real numbers to itself such that for every $x$ and $y$ $$ f(x^2-y^2) = (x-y) (f(x) + f(y)) .$$

• Solution (posted October 15th)

  The problem for week six was taken from the 2000 Korean Mathematical Olympiad. The solution was given in Crux Mathematicorum 31-2 pp 97-98. Solution by P. Bornsztein, France.

  The solution is the set of linear functions passing through the origin.

  Let $f$ be a function satisfying the given functional equation. Setting $ x = y = 0$ in this equation leads to $f(0) = 0.$ Then, setting $y = -x$ gives $0 = f(0) = 2x (f(x) + f(-x)),$ from which we deduce that $f$ is an odd function.

  For all $x$ and $y$, we have $$ f(x^2-y^2) = (x-y)(f(x) + f(y))$$ and also (replacing $y$ by $-y$ , and noting that $f(-y) = - f(y),$ $$ f(x^2-y^2) = (x+y) (f(x) - f(y));$$ that is $yf(x) = x f(y).$ Setting $y=1,$ we get $f(x) = x (f(1))$. Thus, $f$ is linear.

  Conversely, it is easy to verify that any linear function passing through the origin is a solution of the problem.

Week 5

• Problem (posted October 1st)

  For week five there are two rather different problems, with short solutions.

  First Question

  Of Melissa's ducks, $x$ percent have $11$ ducklings each, $y$ percent have $5$ ducklings each and the rest have $3$ ducklings each. The average number of ducklings per duck is $10$. Determine all integer values of $x$ and $y$.

  Second Question

  Let $f(x)$ be a function which satisfies $$ f(29+x) = f(29-x),$$ for all values of $x$. If $f(x)$ has exactly three real roots $\alpha , \beta , \gamma ,$ determine the value of $ \alpha + \beta + \gamma .$
• Solution (posted October 8th)

  Solution of first problem for week 5. This problem was taken from Round 2 of the 2010 Alberta High School Mathematics Competition. Here is the 'official' solution.

  We have $11 x + 5 y+ 3 (100 - x-y) = 1000,$ or $4x+y =350$. Since $y \geq 0$, we get $x \leq 87$. Since $x+y \leq 100,$ we also have that $3x \geq 250$, so $x \geq 84.$ Thus the only solutions in integers are $(x,y) = (84,14),(85,10), (86,6)$ and $(87,2)$.

  Solution of the second problem for week 5. This question is from the Singapore Mathematical Olympiad 2002 with the solution given in Crux Mathematicorum Vol 32-6 p378. Solution by G. Krimker, Buenos Aires.

  Since $f$ has exactly three real roots and $f$ has the same value at points symmetric about $29$, one of the roots must be $29$. Let $ \gamma = 29$. The other two roots, $\alpha$ and $\beta$, must be symmetric about $29$. Hence $\alpha = 29 + x$ and $\beta = 29 -x $, for some real number $x \neq 0.$ Therefore $$ \alpha + \beta + \gamma = (29 + x ) + ( 29 -x ) + 29 =87.$$

Week 4

• Problem (posted September 24th)

  The fourth week problem is about prime numbers, and should be fun.

  Let $a, b, c, a+b-c, b+c-a, a+c-b, a+b+c$ be $7$ distinct prime numbers such that the sum of two of $a,b,c$ is $800.$ Let $d$ be the difference between the largest and the smallest numbers among the $7$ primes. Find the largest possible value of $d$.

• Solution (posted October 1st)

  The problem for week four was taken from the Olympiad Corner in Crux Mathematicorum. It was originally from the 16th China Mathematical Olympiad. The solution appeared in Crux vol 32 issue 5 p. 287.

  Solution by Pierre Bornsztein, France

  The largest possible value of $d$ is 1594. First note that if one of $a,b,c$ is $2$, say $a=2$, then $b$ and $c$ are odd so that $a+b+c$ is even and greater than $2$, which contradicts the hypothesis that it is a prime. Thus $a,b,c\geq 3$ and all seven primes are odd.

  Without loss of generality, we may assume that $a+b =800$ and that $a<b$. Since $a+b-c \geq 3$, we deduce that $c \leq 797.$ Clearly the greatest of the primes is $a+b+c$. Therefore $$d \leq (a+b+c)-3 \leq 800 +797 -3 = 1594.$$

  Conversely, note that $800 + 797 = 1597$ is a prime. And $797$ is a prime too. Thus if $a = 13, b = 787$ and $ c = 797$, it follows that $a+b+c =1597,$ $a+b-c =3$, $a+c-b = 23$ and $b+c-a = 1571$ are all primes. And in that case $d = 1594.$

Week 3

• Problem (posted September 17th)

  Now an algebra problem for the third week.

  Let $ a$, $b$ and $c$ be distinct non-zero real numbers such that $$\frac{1-a^3}{a} = \frac{1-b^3}{b}= \frac{1-c^3}{c}.$$ Determine all possible values of $a^3 + b^3 +c^3$.

• Solution (posted September 24th)

  The third week problem came from Round 2 of the 2007 Alberta High School Mathematics Competition. We give solutions from two of the contestants that were featured in the report on the competition.

  First Solution by Brett Baek

  From $\frac{1-a^3}{a}= \frac{1-b^3}{b}$, we have $ b-a^3 b = a -a b^{3}$. Hence $a-b =ab(b^2-a^2)$ so that $ab(a+b) = -1.$ Similarly, $bc(b+c) = -1.$ From these two equations, we have $a^2 -c^2 = bc -ab$ or $(a+c)(a-c) = -b(a-c).$ Since $a \neq c $, we have $a+b+c = 0$. Hence $abc(a+b) = -c = a+b.$ Since $a+b+c =0$ but $c \neq 0,$ $a+b \neq 0$ and we have $abc =1.$ Now $$ 0 = (a+b+c)^3 = a^3 + 3 a^2(b+c) +3a (b+c)^2 + (b+c)^3 = (a^3 +b^3 + c^3) + 3(a+b+c)(bc+ca+ab)-3abc$$ $$ = (a^3 +b^3 +c^3) + 0 - 3.$$ It follows that the only possible value of $a^3+b^3+c^3$ is $3.$

  Alternate Solution by Jerry Lo
  For those with more knowledge of algebra, this problem is practically trivial.

  The given conditions show that $a,b$ and $c$ are roots of the equation $x^3 +kx -1=0$, where $k$ is the common value of the three fractions. Hence $$ x^3 +kx +1 = (x-a)(x-b)(x-c) = x^3 - (a+b+c) x^2 + (bc+ca+ab)x -abc$$ It follows that $a+b+c=0$, $abc = 1$ and $a^3+b^3+c^3 = (a+b+c)(a^2+b^2+c^2-bc-ca-ab)+3abc =3.$

Week 2

• Problem (posted September 10th)

  For the second week, we give a game for you to figure out.

  A game is played on a $7 \times 7$ board, initially blank. Betty Brown and Greta Green make alternate moves, with Betty going first. In each of her moves, Betty chooses any four blank squares which form a $2 \times 2$ block, and paints these squares brown. In each of her moves, Greta chooses any blank square and paints it green. They take alternate turns until no more moves can be made by Betty. Then Greta paints the remaining blank squares green. Which player, if either, can guarantee to be able to paint 25 or more squares in her colour, regardless of how her opponent plays?
• Solution (posted September 17th)

  The second week problem appeared on Round 2 of the Alberta High School Mathematics Competition 2009. This is adapted from the 'official solution'.

  There are $9$ squares at the intersections of even-numbered rows and even-numbered columns.

  	*		*		*
  	*		*		*
  	*		*		*

  Any $2 \times 2$ block chosen by Betty must include one of these nine squares. Greta should play only on these squares in her first four moves. This will ensure that Betty has at most five moves, and can paint at most 20 squares brown. Then Greta wins since she paints 29 squares green.

Week 1

• Problem (posted September 3rd)

  For the first question, we look at a puzzle type problem that involves little calculation, but some reasoning. Look next week to check your solution.

  In a hockey tournament, five teams participated where each team played against each other team exactly once. A team receives $2$ points for a win, $1$ point for a tie and $0$ points for a loss. At the end of the tournament the results showed that no two teams received the same total points, and the order of the teams (from highest point total to lowest point total) was $A,B,C,D,E$. Team $B$ was the only team that did not lose any games and team $E$ was the only team that did not win any games. How many points did each team receive and what was the result of each game?

  	Total Points
  $A$
  $B$
  $C$
  $D$
  $E$

  	Winner (or tie)
  $A$ vs $B$
  $A$ vs $C$
  $A$ vs $D$
  $A$ vs $E$
  $B$ vs $C$
  $B$ vs $D$
  $B$ vs $E$
  $C$ vs $D$
  $C$ vs $E$
  $D$ vs $E$
• Solution (posted September 10th)

  The first week's problem appeared on the 2013 Calgary Junior Mathematics Contest. Here is the 'official' solution.

  	Total Points
  $A$	6
  $B$	5
  $C$	4
  $D$	3
  $E$	2

  	Winner (or tie)
  $A$ vs $B$	$B$
  $A$ vs $C$	$A$
  $A$ vs $D$	$A$
  $A$ vs $E$	$A$
  $B$ vs $C$	$T$
  $B$ vs $D$	$T$
  $B$ vs $E$	$T$
  $C$ vs $D$	$C$
  $C$ vs $E$	$T$
  $D$ vs $E$	$D$

  Note that if we total the points for each match we obtain $2$, so the point total recorded for the $10$ games is $20$. Since $B$ was the only team that did not lose a game, $A$ lost at least one game, making its maximum possible point total $6$. Its point total could not be $5$ since $5+4+3+2+1 = 15 < 20$. Thus Team $A$ has three wins and one loss. Since $B$ has no losses the game $A$ lost must have been to $B$. Then $B$ must have a tie in all three of its other games (otherwise, it has at least 6 points, at least as many as $A$). All the teams but $E$ won some games, so both $C$ and $D$ won some game. Neither of them could win both games (excluding those with $A$ and $B$ about which we already know) because that would give a point total of $5$ which $B$ got. Thus $C$ won one of the other games and had one tie, and $D$ won one game and had one loss, which means that $E$ had one loss and one tie in the remaining games. Thus $E$ lost the game with $D$ and had a tie with $C$.