Le Défi ouvert canadien de mathématiques 2018 — nov. 8/9

Nicolae Strungaru
Problème de la semaine
— Nicolae Strungaru, Grant MacEwan University
Les problèmes du DOCM se divisent en trois parties. Pour la partie A, il n'est pas nécessaire d'écrire ses démarches dans la solution. Il est même possible de résoudre les problèmes sans avoir à écrire quoi que ce soit. Les problèmes de la partie B présentent un défi plus élevé et nécessitent des connaissances un peu plus poussées. Pour ceux-ci, vous aurez sans doute besoin de papier et d'un crayon. Les problèmes de la partie C nécessitent des réponses complètes avec justification pour les arguments proposés.
Nous avons sélectionné une variété de problèmes provenant de divers concours nationaux et régionaux avec l'espoir de susciter votre intérêt pour la résolution de problèmes et vous donner un peu de préparation pour le Défi ouvert canadien de mathématiques en novembre. Les problèmes touchent à large éventail de domaines mathématiques (algèbre, logique, géométrie...) mais ne sont pas associés à un âge scolaire précis.
Nous publierons les solutions aux problèmes la semaine suivante. Nous avertissons toutefois les enseignants qu’il se pourrait que des étudiants déterminés trouvent les solutions ailleurs en ligne avant qu’elles ne soient publiées ici.
Pour obtenir d’autres ensembles de problèmes et de solutions à chacun de ces niveaux, n’hésitez pas à télécharger les anciens examens officiels et leurs solutions dans nos archives.
Semaine 9
-
Problème
(publié le
30 octobre)
Cette semaine, on s'intéresse à une inégalité géométrique.
Les points $D$ et $E$ sont choisis sur les côtés $AB$ et $AC$ du triangle $ABC$ de façon à ce que $DE$ soit parallèle à $BC$ et tangent au cercle inscrit au $\Delta ABC$. Démontrer que $$DE \leq \frac{1}{8} \left(AB+AC+BC \right).$$
-
Solution
(publié le
6 novembre)
Problème 2 du concours pour la sélection de l'équipe italienne de 1999, apparu dans le Crux Mathematicorum [2002:356-357]. On présente la solution de Toshio Seimiya apparue dans l'édition [2004:492].
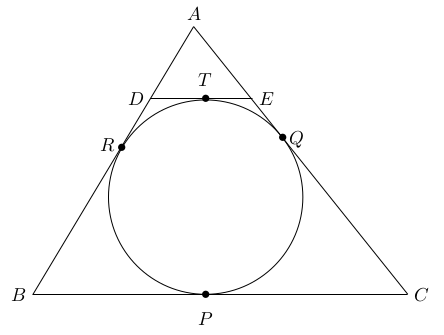
On pose $BC=a, AC=b, AB=c$. Soit $P,Q,R$ respectivement les points de rencontre du cercle inscrit avec les segments $BC, CA$ et $AB$. On note aussi $T$ le point où $DE$ est tangent au cercle.
Puisque $DE \parallel BC$ on a $\Delta ADE \sim \Delta ABC$ et donc
(4) $\frac{AD+DE+EA}{AB+BC+CA}=\frac{DE}{BC}=\frac{DE}{a}.$ Ensuite, les tangentes au cercle passant par $D$ sont congrues et les tangentes au cercle passant par $E$ le sont aussi. Ainsi,
$DT$ $=DR$ $ET$ $=EQ.$ On a donc
(5) $AD+DE+EA=AQ+AR.$ Ensuite, en utilisant à nouveaux que les tangentes à partir de $A,B$ et $C$ respectivement sont congruentes, on trouve
$AR$ $=AQ$ $BR$ $=BP$ $CQ$ $=CP.$ Ainsi $$b+c-a=AR+BR+AQ+CQ-BP-CP=AR+AQ.$$
Donc, par (5) on trouve $$AD+DE+EA=AQ+AR=b+c-a.$$
En mettant cette équation dans (4) on trouve $$\frac{b+c-a}{b+c+a}=\frac{DE}{a}.$$
Donc $$DE=\frac{a(b+c-a)}{(b+c+a)}.$$
Alors
$\frac{1}{8} \left( AB+BC+CA \right)-DE$ $= \frac{1}{8}(a+b+c)- \frac{a(b+c-a)}{(b+c+a)}$ $=\frac{1}{8(a+b+c)} \left( (a+b+c)^2-8a(b+c-a) \right)$ $=\frac{1}{8(a+b+c)} \left( a^2+2a(b+c)+(b+c)^2-8a(b+c)+8a^2 \right)$ $=\frac{1}{8(a+b+c)} \left( 9a^2-6a(b+c)+(b+c)^2 \right)$ $=\frac{1}{8(a+b+c)} \left( 3a- (b+c) \right)^2 \geq 0.$ Ainsi, $$DE \leq \frac{1}{8} \left(AB+AC+BC \right).$$
Semaine 8
-
Problème
(publié le
23 octobre)
Cette semaine, on s'intéresse à une équation avec des nombres premiers.
Trouver tous les nombres premiers $p$ et $q$ tels que $$p^2-p+1=q^3.$$
-
Solution
(publié le
30 octobre)
Problème 4 du test 1 de la 25ème Olympiade mathématique d'Albanie, apparu dans le Crux Mathematicorum [2007:278-279]. On présente la solution de Titu Zvonaru, apparue dans l'édition [2008:220].
On démontre que la seule solution est $p=19, q=7$, ce qui nous donne $$19^2-19+1=343=7^3.$$
Commençons par observer que $$q^3 = p^2-p+1 < p^2 < p^3 \,,$$ et donc $q < p$.
On peut réécrire l'équation comme suit:
(2) $p(p-1)=(q-1)(q^2+q+1).$ Puisque $p$ est premier, (2) implique que $p|q-1$ ou $p|q^2+q+1$. Il est impossible que $p|q-1$ car $p>q>q-1>0$ et donc il doit y avoir un entier $k$ tel que
(3) $q^2+q+1=pk.$ En combinant (2) et (3) on trouve $$p-1=k(q-1)$$ et donc $$p=k(q-1)+1.$$
Ainsi, par (3) on trouve $$q^2+q+1=k^2q-k^2+k.$$
La valeur $q$ est donc une solution à l'équation du deuxième degré $$q^2+(1-k^2)q+(k^2-k+1)=0.$$
Comme $q$ est un entier et que l'équation est à coefficients entiers, le discriminant $$\Delta= (k^2-1)^2-4(k^2-k+1) \,,$$ doit être un carré parfait.
Finalement, comme $k$ est un entier strictement positif, on sait que $\Delta < (k^2-1)^2$, $\Delta$ et $(k^2-1)^2$ ont la même parité. On en déduit que $\Delta \leq(k^2-3)^2$.
Ainsi
$(k^2-1)^2-4(k^2-k+1)$ $\leq (k^2-3)^2$ $k^4-2k^2+1-4k^2+4k-4$ $\leq k^4-6k^2+9$ $4k$ $\leq 12$ $k$ $\leq 3.$ Puisque $k$ est un entier strictement positif, $k \in \{1 ,2 , 3 \}$.
Maintenant, $k=1$ et $k=2$ nous donnent respectivement $\Delta=-4$ et $\Delta=-3$ ce qui n'est pas possible. La seule possibilité est donc $k=3$ qui nous mène à $\Delta=36$ et $$q=\frac{8 \pm 6}{2}.$$
Puisque $q$ est premier, $q=7$ et $$p=\frac{q^2+q+1}{k}=\frac{57}{3}=19.$$
Ainsi, $$p=19 \,;\, q=7.$$
Semaine 7
-
Problème
(publié le
16 octobre)
Cette semaine, la question concerne la construction de rectangles de différentes formes. Ce type de construction est souvent appelé « pavage ».
Démontrer qu'un rectangle $m \times n$ peut être construit en utilisant des copies de la forme suivante (sans chevauchement) si et seulement si $m,n >1$ et $8 | mn$.
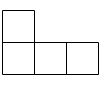
-
Solution
(publié le
23 octobre)
Problème 5 de l'Olympiade mathématique de Corée 2000, apparu dans le Crux Mathematicorum [2003:22-23]. On présente la solution légèrement modifiée de Pierre Bornsztein, apparue dans l'édition [2005:99-100].
Une figure de la forme donnée s'appelle un « tétramino ».
On commence par démontrer que si un rectangle $m \times n$ peut être construit en utilisant des tétraminos, alors $m,n >1$ et $8|mn$. L'affirmation selon laquelle $m,n >1$ est triviale.
Puisque le rectangle a une aire $mn$ et qu'un tétramino a une aire de $4$, il est certain que $mn=4k$ où $k$ est le nombre de tétraminos utilisés. On doit maintenant montrer que $k$ est pair.
Colorions les rangées du rectangle $m \times n$ en noir et blanc en alternant les couleurs, de façon à ce que les rangées impaires soient blanches et que les rangées paires soient noires.
Puisque $4|mn$, soit $m$ ou $n$ doit être pair et donc le nombre de cases blanches doit être pair (et le nombre de cases noires aussi par le fait même).
Maintenant, peu importe la position et l'orientation du rectangle, il est clair qu'un tétramino doit être posé sur une ou trois cases blanches. On pose $t$ le nombre de tétraminos posés sur 3 cases blanches. Les autres $k-t$ tétraminos sont donc posés sur une seule case blanche.
Comme le nombre de cases blanches est pair, on trouve $$3t+(k-t)=k-2t \mbox{ est pair }.$$
Ceci implique que $k$ est pair et donc que $mn=4k$ est divisible par $8$.
Maintenant, on montre que si $m,n >1$ et $8|mn$ alors un rectangle $m \times n$ peut être construit avec des tétraminos.
Remarquons tout d'abord qu'un rectangle $2 \times 4$ et un rectangle $3 \times 8$ peuvent être construits avec des tétraminos, comme dans on le montre ici :
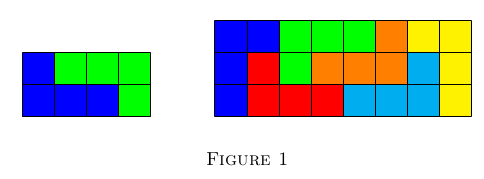
En retournant possiblement le rectangle de $90^\circ$, on peut supposer que soit (i) $4|n$ et $2|m$ ou (ii) $8 |n$.
Dans le cas (i), on peut construire le rectangle en utilisant $\frac{mn}{8}$ copies du rectangle $4 \times 2$ montré à la figure 1.
Occupons nous maintenant du cas $8|n$.
Si $m$ est pair, alors nous sommes dans la situation (i) et on peut facilement construire le rectangle avec $\frac{mn}{8}$ copies du rectangle $4 \times 2$ de la figure 1.
Si $m$ est impair, puisque $m \neq 1$, on a $m \geq 3$. Alors $m-3=2k$ pour un certain entier $k \geq 0$.
Puisque $8 |n$, on peut construire un rectangle $3 \times n$ à partir du rectangle $3 \times 8$ de la figure 1.
On peut aussi construire un rectangle $2 \times n$ avec des copies du rectangle $2 \times 4$ de la figure 1.
Ainsi, en utilisant un rectangle $3 \times n$ et $k$ copies d'un rectangle $2 \times n$, on peut construire un rectangle $m \times n$.
Semaine 6
-
Problème
(publié le
9 octobre)
Cette semaine, on s'intéresse à un problème de géométrie.
Soit $ABC$ un triangle aigu avec $\angle B = \angle C$. Soit $O$ le centre du cercle circonscrit et $H$ l'orthocentre de $\Delta ABC$. Démontrer que le centre du cercle $BOH$ repose sur le segment $AB$.
-
Solution
(publié le
16 octobre)
Problème 2 de la ronde 2 de l'Olympiade mathématique 2008-2009, apparu dans le Crux Mathematicorum [2011:352-353]. On présente la solution d'Oliver Geupel apparue dans l'édition [2012:270].
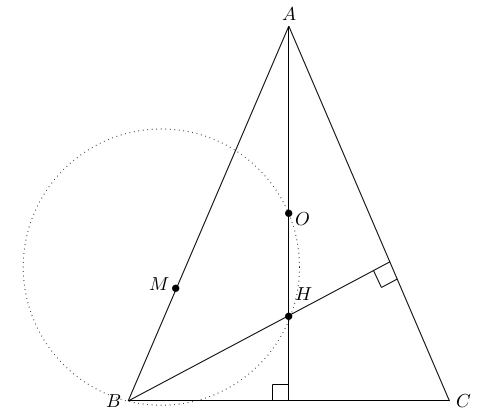
Puisque $AC$ est perpendiculaire à la hauteur $BH$, on a $$\angle ABH = 90^\circ - \angle A.$$
Soit $M$ le centre du cercle $BOH$. Alors $$\angle MBH = 90^\circ - \frac12 \angle BMH = 90^\circ - \angle BOH.$$
Puisque $\angle B = \angle C$, it holds $$\angle BOH = \frac12 \angle BOC = \angle A.$$
On en déduit que $$\angle ABH = \angle MBH,$$ et donc les points $A$, $B$ et $M$ sont colinéaires.
Semaine 5
-
Problème
(publié le
2 octobre)
Cette semaine, on s'intéresse à une équation fonctionnelle.
Notons $\mathbb{Q}$ l'ensemble des nombres rationnels. Trouver toutes les fonctions $f: \mathbb{Q} \to \mathbb{Q}$ telles que
(1) $f\left(x+f(y)\right)=y+f(x) \qquad \forall x,y \in \mathbb{Q}.$ -
Solution
(publié le
9 octobre)
Problème 8 de la 15ème Olympiade mathématique d'Irlande, apparu dans le Crux Mathematicorum [2005:437-439]. On présente la solution de Mohammed Aassila apparue dans l'édition [2007:33].
En posant $x=0$ dans (1) on obtient $$ f(f(y))=y+f(0) \qquad \forall y \in \mathbb{Q}. $$
On affirme que $f$ est une bijection. En effet, si $f(a)=f(b)$ alors $$ a+f(0)=f(f(a))=f(f(b))=b+f(0) \,,$$ et donc $a=b$.
Ensuite, en posant $y=0$ dans (1) on obtient $$f(x+f(0))=f(x).$$
Puisque $f$ est une bijection, on sait que $x+f(0)=x$ et donc $$f(0)=0.$$
Ainsi, on a aussi que $$f(f(y))=y \qquad \forall y \in \mathbb{Q}.$$
Ensuite, en remplaçant $y$ par $f(y)$ dans (1) et en utilisant $f(f(y))=y$ on trouve $$f(x)+f(y)=f(x+f(f(y))=f(x+y) \qquad \forall x, y \in \mathbb{Q}.$$
Il s'agit de la fameuse équation fonctionnelle de Cauchy, ce qui implique que, en prenant $a=f(1) \in \mathbb Q$, on a $f(x)=ax \, \forall x \in \mathbb{Q}$.
Ensuite, puisque $f(f(y))=y \, \forall y \in \mathbb{Q}$ on a $a=\pm 1$.
insi, il y a seulement deux solutions possibles à cette équation: $f(x)=x \, \forall x \in \mathbb{Q}$ et $f(x)=-x \, \forall x \in \mathbb{Q}$.
Il est facile de vérifier que $f(x)=x$ et $f(x)=-x$ sont réellement des solutions à (1).
Note : Pour le lecteur moins familier avec l'équation fonctionnelle de Cauchy, on la résout ici.
Soit $f: \mathbb{Q} \to \mathbb{Q}$ tel que $$f(x+y)=f(x)+f(y) \qquad \forall x,y \in \mathbb Q$$ et posons $a:=f(1)$.
Puisque $f(x+y)=f(x)+f(y)$, un argument d'induction facile démontre que $f(nx)=nf(x) \, \forall x \in \mathbb Q, n \in \mathbb N$. De plus, $$ 0=f(0)=f(x-x)=f(x)+f(-x) \,,$$ et il en suit que $f$ est une fonction impaire et que $$f(nx)=nf(x) \qquad \forall x \in \mathbb Q, n \in \mathbb Z.$$
Soit $x \in \mathbb Q$ une valeur arbitraire et écrivons $x= \frac{m}{n}$ avec $m,n \in \mathbb{Z}$ et $n >0$. Alors, $$a=f(1)=f(n \cdot \frac{1}{n})=n f(\frac{1}{n}) \Rightarrow f(\frac{1}{n})=\frac{a}{n} \,,$$ et donc $$f(x)=f(\frac{m}{n})=f(m \cdot \frac{1}{n})=m f(\frac{1}{n}) =m \frac{a}{n}=ax.$$
Ceci montre que $f(x)=ax$ pour tout $x \in \mathbb{Q}$.
Semaine 4
-
Problème
(publié le
25 septembre)
Cette semaine, le problème concerne un polynôme à coefficients entiers.
Étant donné $n$ entiers distincts $m_1,...,m_n$, démontrer qu'il existe un polynôme $P(X)$ de degré $n$ à coefficients entiers qui satisfait les conditions suivantes :
- $P(m_k)=-1$ pour tout $1 \leq k \leq n$.
- $P(X)$ est irréductible en $\mathbb{Z}[X]$, ce qui veut dire que $P(X)$ ne peut être écrit comme le produit de deux polynômes non constants à coefficients entiers.
-
Solution
(publié le
2 octobre)
Problème 4 de la 4ème Olympiade mathématique de la République de Chine (Taiwan), apparu dans le Crux Mathematicorum [1998:322-323]. On présente la solution de Pierre Bornsztein, apparue dans l'édition [2000:75].
Il est facile de voir que $$ P(X)=(X-m_1)(X-m_2)..(X-m_n)-1 $$ a des coefficients entiers et est de degré $n$. Pour compléter la preuve, on doit montrer que $P(X)$ satisfait la condition (ii).
Supposons par contradiction qu'on peut trouver $Q,R \in \mathbb{Z}[X]$ de degré au plus $n-1$ tels que $$ P(X)=Q(X)\cdot R(X). $$
Alors, pour chaque $1 \leq k \leq n$ on a $$ Q(m_k)\cdot R(m_k)=-1. $$
Ceci implique que soit $Q(m_k)=1, R(m_k)=-1$ ou que $Q(m_k)=-1, R(m_k)=1$. On sait alors que $$ Q(m_k)+R(m_k)=0 \qquad \forall 1 \leq k \leq n. $$ On en déduit donc que $Q(X)+R(X)$ est un polynôme de degré au plus $n-1$ qui possède $n$ racines distinctes. Ainsi, $$ Q(X)+R(X) \equiv 0. $$
On en déduit que $R(X)=-Q(X)$ et donc que $$ P(X)=-\left( Q(X) \right)^2. $$
Ceci est impossible puisque le coefficient directeur de $P(X)$ est $1$. Nous avons donc une contradiction.
Cette contradiction nous indique que l'hypothèse selon laquelle $P(X)$ est réductible est fausse, et donc $P(X)$ est irréductible dans $\mathbb{Z}[X]$ comme voulu.
Semaine 3
-
Problème
(publié le
18 septembre)
Cette semaine on s'intéresse à des aires de trapèzes.
Les deux diagonales d'un trapèze le divisent en quatre triangles. Les aires de trois des triangles sont 1, 2 et 4 unités carrées. Quelles sont les valeurs possibles pour l'aire du quatrième triangle?
-
Solution
(publié le
25 septembre)
Problème 19 du 19ème Concours Lituanien par équipe, apparu dans le Crux Mathematicorum [2008:282-284]. On présente la solution de George Tsapakidis apparue dans l'édition [2009:303].
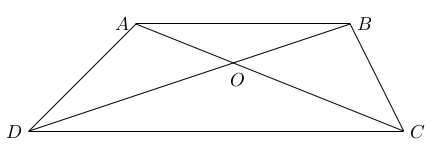
Pour un triangle dont les sommets sont $X,Y$ et $Z$, la notation $[XYZ]$ signifiera l'aire du triangle.
Puisque $\Delta ABD$ et $\Delta ABC$ ont la même base $AB$ et la même hauteur par rapport à cette base, ils ont la même aire. Ainsi, $$[OAD]+[OAB]=[ABD]=[ABC]=[OBC]+[OAB].$$
On obtient donc que $[OAD]=[OBC]$.
Puisque la hauteur passant par $B$ relative aux segments $AO$ et $OC$ est la même, on a $$\frac{[AOB]}{[BOC]}=\frac{AO}{CO}.$$
De la même façon, la hauteur par $D$ relative aux segments $AO$ et $OC$ est la même et on en déduit $$\frac{[DOA]}{[DOC]}=\frac{AO}{CO}.$$
Ainsi, $$[DOA]\cdot [BOC] = [DOC] \cdot [AOB].$$
Puisque $[AOD]=[BOC]$ et que trois des aires sont $1,2$ et $4$, on en déduit que $$[AOD]=[BOC] =2.$$ Le quatrième triangle a donc une aire de $2$ unités carrées.
Semaine 2
-
Problème
(publié le
11 septembre)
Cette semaine, nous nous intéressons à un problème qui consiste à colorier les entiers strictement positifs.
Chaque entier strictement positif est colorié soit en rouge ou en vert de façon à ce que les trois conditions suivantes soient satisfaites.
- La somme de 3 nombres rouges (pas nécessairement distints) est rouge.
- La somme de 3 nombres verts (pas nécessairement distints) est verte.
- Il y a au moins un nombre colorié de chaque couleur.
Déterminer tous les coloriages possibles.
-
Solution
(publié le
18 septembre)
Problème 2 du Bundeswettbewerb Mathematik 2007, apparu dans le Crux Mathematicorum [2010:22]. On présente la solution de Titu Zvonaru, apparue dans l'édition [2011:31].
Soit $R$ l'ensemble de tous les nombres rouges et $V$ l'ensemble de tous les nombres verts.
Tout d'abord, démontrons par induction que si $a \in R$ et que $n$ est un entier positif, alors $(2n+1)\cdot a \in R$. L'étape initiale $P(0): (2 \cdot 0+1)\cdot a \in R$ est vraie par l'hypothèse de départ. L'étape d'induction suit : $$(2(n+1)+1)\cdot a =((2n+1)\cdot a)+a+a$$ est la somme de trois éléments de $R$ et doit donc appartenir à $R$.
De la même façon, on peut montrer par induction que si $b \in V$ et que $n$ est un entier positif, alors $(2n+1)\cdot b \in V$.
La condition (iii) nous indique qu'il existe $a \in R, b\in V$. Par les résultats précédents, $R$ et $V$ sont infinis.
On sait que $1 \in R$ ou que $1 \in V$. Il est suffisant d'étudier le cas $1 \in R$ puisque le cas contraire consiste seulement à inverser les couleurs.
Pour le reste de la démonstration, nous supposerons alors que $1 \in R$. Nous allons montrer que $R$ est l'ensemble de tous les entiers positifs impairs, et donc que $V$ est l'ensemble de tous les entiers strictement positifs pairs.
Puisque $1 \in R$, le résultat démontré plus tôt nous dit que $(2k+1)\cdot 1 \in R$ et donc que $R$ contient tous les entiers positifs impairs.
Supposons par contradiction que $R$ contient un entier de la forme $2m$. Ainsi, pour tout $n >m$ nous avons $$2n=2m+(2(n-m-1)+1)+1 \in R.$$
Ainsi, $R$ contient tous les entiers positifs impairs ainsi que tous les entiers pairs supérieurs à $2m$. Par contre, cela contredit le fait que $V$ est infini.
Puisque nous avons obtenu une contradiction, notre hypothèse selon laquelle $R$ contient un entier pair est erronée.
Il s'en suit que $R$ est formé de tous les entiers positifs impairs et que $V$ est formé de tous les entiers pairs strictement positifs.
Réponse : Il y a exactement deux coloriages possibles :
- Tous les entiers positifs impairs sont verts et les autres sont rouges.
- Tous les entiers positifs impairs sont rouges et les autres sont verts.
Semaine 1
-
Problème
(publié le
4 septembre)
Voici deux problèmes plus simples pour cette première semaine.
Problème A
Déterminer la somme de tous les entiers $n$ tels que $2009+n^2$ est le carré d'un entier positif.Problème B
La figure suivante montre trois carrés. Déterminer la mesure de l'angle $\alpha +\beta$.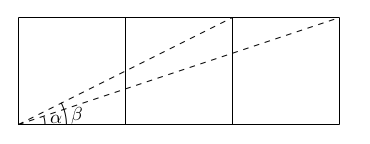
-
Solution
(publié le
11 septembre)
Problème A
Problème 8 du concours mathématique Niels Henrik Abel 2008-2009, apparu dans la section Skoliad du Crux Mathematicorum [2009:481-483]. On présente la solution de Lena Choi, publiée dans l'édition [2010: 358].
Si $$n^2+2009=x^2$$ alors $$x^2-n^2=(x-n)(x+n)=2009.$$
Puisque $2009=41 \cdot 7^2$, $2009$ peut être écrit comme un produit de deux entiers positifs de seulement trois façons différentes.
$2009=1$ · $2009$ $2009=7$ · $287$ $2009=41$ · $49.$ Puisque $x$ et $n$ sont tous deux positifs, $x+n >x-n$. Ainsi, nous avons les solutions
$x+n = 2009$ $x-n= 1$ ⇒ $n=1004$ $x+n = 287$ $x-n= 7$ ⇒ $n=140$ $x+n = 49$ $x-n= 41$ ⇒ $n=4$. Leur somme est $$1004+140+4=1148.$$
Problème B
Problème 5 de la finale junior ronde B du BC Colleges High School Mathematics Contest, apparu dans la section Skoliad du Crux Mathematicorum [2004:385-387]. On présente la solution d'Alex Wise ainsi qu'une adaptation mineure de la solution officielle publiée dans l'édition [2005: 135].
Première solution
On a $\tan(\alpha)=\frac{1}{3}$ and $\tan(\beta)=\frac{1}{2}$. Ainsi, $$\tan(\alpha+\beta)= \frac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}=\frac{\frac{1}{3}+\frac{1}{2}}{1-\frac{1}{6}}=1.$$
Puisque $\alpha$ et $\beta$ sont aigus, on sait que $0 < \alpha +\beta <180^\circ$ et ainsi $\alpha+\beta=45^\circ$.
Deuxième solution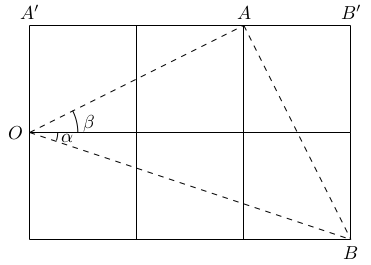
Si nous r\'earrangeons les carrés comme dans l'image, on trouve que $\Delta OA'A \equiv \Delta AB'B$ et donc
$OA$ $=$ $AB$ $\angle OAA'+ \angle BAB'$ $=$ $\angle OAA'+\angle AOA'=90^\circ.$ Ainsi, $\Delta OAA'$ est un triangle rectangle isocèle et donc $$\alpha+\beta =45^\circ.$$
Correction du Problème A:La version francophone du problème contient une erreur puisque le problème original fait référence aux entiers positifs seulement. Lorsque tous les entiers sont admis, si $n$ est une solution alors $-n$ est aussi une solution et la somme doit être $0$. Ce raisonnement est valide lorsque le nombre de solutions est fini, ce qui est bien le cas dans ce problème.
Pour signaler des erreurs ou des faits manquants pour cette page, veuillez communiquer avec nous au docm@smc.math.ca.
