Le Défi ouvert canadien de mathématiques Financière Sun Life 2015 — nov. 5/6

Robert Woodrow
Problème de la semaine
— Robert Woodrow, président du comité du DOCM 2015
Les problèmes du DOCM se divisent en trois parties. Pour la partie A, il n'est pas nécessaire d'écrire ses démarches dans la solution. Il est même possible de résoudre les problèmes sans avoir à écrire quoi que ce soit. Les problèmes de la partie B présentent un défi plus élevé et nécessitent des connaissances un peu plus poussées. Pour ceux-ci, vous aurez sans doute besoin de papier et d'un crayon. Les problèmes de la partie C nécessitent des réponses complètes avec justification pour les arguments proposés.
Nous avons sélectionné une variété de problèmes provenant de divers concours nationaux et régionaux avec l'espoir de susciter votre intérêt pour la résolution de problèmes et vous donner un peu de préparation pour le Défi ouvert canadien de mathématiques en novembre. Les problèmes touchent à large éventail de domaines mathématiques (algèbre, logique, géométrie...) mais ne sont pas associés à un âge scolaire précis.
Nous publierons les solutions aux problèmes la semaine suivante. Nous avertissons toutefois les enseignants qu’il se pourrait que des étudiants déterminés trouvent les solutions ailleurs en ligne avant qu’ils soient publiés ici.
Pour obtenir d’autres ensembles de problèmes et de solutions à chacun de ces niveaux, n’hésitez pas à télécharger les anciens examens officiels et leurs solutions dans nos archives.
Semaine 9
-
Problème
(publié le
27 octobre)
On définit la fonction $t(n)$ sur les entiers positifs par $t(0) = t(1) = 0$, $t(2) = 1$ et pour les entiers $n>2$, $t(n)$ est le plus petit entier strictement positif qui ne divise pas $n$. Soit $T(n) = t(t(t(n))).$ Déterminez la valeur de $S$: $$ S = T(1) + T(2) + T(3) + \cdots +T(2006).$$
-
Solution
(publié le
3 novembre)
Il s'agit du problème 1 de la ronde finale des Olympiades mathématiques de Hongrie, édition 2005-2006 pour les étudiants de niveau 11-12. Le problème a aussi été donné dans le Crux Mathematicorum [2009:211-212]. La solution donnée ici est une modification de celle de Michel Bataille de Rouen en France, aussi donnée dans l'édition [2010:281]
On remarque premièrement que $T(n) = 0$ si $n = 2$ ou si $n$ est un entier impair. On peut donc réduire à $S = T(4) + T(6) + \cdots T(2006).$
Si $n \in \mathbb{P} = \{4,6,8, \cdots, 2006\}$ et $n$ est un multiple de $3$, alors $t(n) =3$ et $T(n) =1.$
Soit $\mathbb{P}_1 = \{6, 18,30, \cdots 6 \cdot 333 \}$ les éléments de $\mathbb{P}$ de la forme $6(2m-1)$ et $\mathbb{P}_2$ les éléments de $\mathbb{P}$ de la forme $12m$.
Pour tout $n \in \mathbb{P}_1,$ on sait que $t(n)=4$ et alors que $T(n) = 2$. De plus, on trouve qu'il y a $167 $ nombres dans $\mathbb{P}_1.$
Si $n \in \mathbb{P}_2$ et que $n$ n'est pas un multiple de $5$ ou $n$ n'est pas un multiple de $7$ , alors $t(n) = 5 $ ou $t(n) = 7$. On a donc que $T(n) =1$. Il ne reste que quelques nombres dont on n'a pas encore calculé la valeur de $T$: $T(420) = 2, T(840)=1, T(1260) = 2,$ et $T(1680) = 1$.
Ainsi, $T(n)=1$ pour chaque $n \in \mathbb{P}_2$, à l'exception de deux nombres pour lesquels $T$ prend la valeur $2$.
Au total, $T(n) = 2 $ pour $167+2=169 $ nombres et $T(n)=1 $ pour les $1002-169 = 833$ nombres restants. Le résultat est alors $S = 833+2 \cdot 169 = 1171.$
Semaine 8
-
Problème
(publié le
20 octobre)
Soit $A$ un point fixé à l'extérieur d'un cercle de centre $O$ et de rayon $r$. Soit $M$ un point sur le cercle, et $N$ le point diamétralement opposé à $M$ par rapport à $O$. Trouvez le lieu géométrique du centre des cercles passant par $A,M$ et $N$ lorsqu'on laisse bouger $M$ sur le cercle.
-
Solution
(publié le
27 octobre)
Il s'agit du problème 2 de la 19e édition de l'Olimpiada Iberoamericana de Matematicas qui a aussi été donné dans la section Olympiad du Crux Mathematicorum [2008:14]. La solution proposée est due à Michel Bataille de Rouen en France et a été donné dans l'édition [2009:219].
Soit $U$ le centre du cercle circonscrit au $\triangle AMN$. Comme $O$ est le point milieu de $MN,\ UO$ est orthogonal à $MN$ et $UM^2 = UO^2 +r^2.$
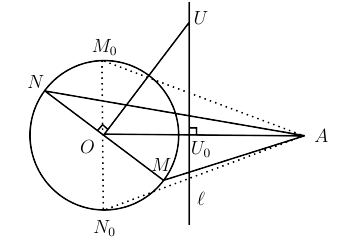
Comme $UM = UA$, on a $UA^2-UO^2=r^2.$ Il en suit que $U$ est sur la droite $\textit{l}$ perpendiculaire à $AO$. Plus précisément, si $M_0N_0$ est le diamètre perpendulaire à $AO$ et $U_0$ est le centre du cercle circonscrit au $\triangle AM_0N_0$, alors $\textit{l}$ est la perpendiculaire à $AO$ passant par $U_0$. On remarque que $U_0 \neq O$.
Prenons $U$ un point sur la droite $l$ (tel que $UA^2 -UO^2 = r^2$), et prenons $MN$ comme le diamètre perpendiculaire à $UO$. Ainsi $UO^2+r^2 = UM^2=UN^2$ de façon à ce que $UM=UN=UA$ et $U$ est sur le cercle circonscrit de $\triangle AMN $ (on remarque que $A,M$ et $N$ ne sont pas colinéaires puisque $U_0 \neq O).$
Semaine 7
-
Problème
(publié le
13 octobre)
Trouvez les valeurs strictement positives de $x$ qui satisfont l'équation $$ x^{(2 \sin x - \cos 2x )} < \frac{1}{x}.$$
-
Solution
(publié le
20 octobre)
Il s'agit du problème 1 des Olympiades mathématiques de Hongrie pour les niveaux 11 et 12 dans l'édition 2005-2006. Le problème a été donné dans la section Olympiad du Crux Mathematicorum [2009:211]. La solution due à Olver Geupel, de Fruhl en Allemagne, a été donnée dans l'édition [2010:280].
Puisque $\cos 2x = 1 - 2 \sin^2 x$ et $x >0$, l'inégalité donnée est équivalente à $x^{2 \sin x (1+ \sin x)} <1.$ On écrit $a = 2 \sin x (1+\sin x).$ Pour $x >0,$ l'inégalité $x^a <1$ tient si et seulement si
(1) $ 0 < x < 1$ et $a>0$, ou
(2) $x>1$ et $a<0.$Si $0 < x < 1$, alors on a $\sin x >0$ et la condition (1) est satisfaite.
Si $x >1$, alors $a < 0$ tient si et seulement si $-1 < \sin x < 0.$ Ainsi, (2) est équivalent à $(2k+1) \pi < x < (2k + \frac{3}{2}) \pi$ ou $(2k+\frac{3}{2} \pi < x < (2k+2)\pi$ pour un entier positif $k$. Conséquemment, l'ensemble solution est l'union de ces intervalles. $$(0,1) \cup \bigcup_{k=0}^\infty \left( (2k+1 )\pi,\left(2k+\frac{3}{2}\right) \pi \right) \cup \bigcup_{k=0}^\infty \left( \left( 2k+\frac{3}{2} \right) \pi,(2k+2)\pi\right)$$
Semaine 6
-
Problème
(publié le
6 octobre)
Soit $f:[0,4] \rightarrow [0,\infty)$, tel que $f(4) =2$ et $f(x+y) \geq f(x) + f(y)$ pour toute paire de nombres réels $x$ et $y$ dans l'intervalle fermé $[0,4]$ pour laquelle $x+y \leq 4.$
(a) Supposons que $0 \leq x \leq y \leq 4.$ Montrez que $f(y) \geq f(x).$
(b) Montrez que $f(x) \leq x$ pour tout $x$ dans $[0,4].$
-
Solution
(publié le
13 octobre)
Il s'agit du problème 3 de l'édition 2014-2015 du ConocoPhillips Alberta High School Mathematics Prize Examination qui a eu lieu en février 2015.
(a) Si $0 \leq x \leq y \leq 4$ alors $f(y) = f(x+(y-x)) \geq f(x) + f(y-x) \geq f(x).$
(b) Si $x$ est dans l'intervalle $[2,4]$, alors $f(x) \leq f(4) = 2 \leq x$. Par contre, si $x$ est dans l'intervalle $(0,2)$, alors $\frac{4}{x} - \frac{2}{x} = \frac{2}{x} >1.$ Ainsi, il y a un entier positif $n$ tel que $\frac{2}{x} < n < \frac{4}{x}$ ou $2 < nx < 4,$ de façon à ce que $f(nx) \leq nx$. De plus, $f(nx) = f((n-1)x+x) \geq f((n-1)x)+f(x) \geq f((n-2)x)+2f(x) \geq \cdots \geq nf(x)$ et donc $f(nx) \geq nf(x).$ Ainsi, $nf(x) \leq f(nx) \leq nx$ et alors $f(x) \leq x$ pour tout $x $ dans l'intervalle $(0,2)$. Conséquemment, $f(x) \leq x$ pour toute valeur de $x$ dans $[0,4]$.
Semaine 5
-
Problème
(publié le
29 septembre)
C'est le moment de faire un peu de géométrie.
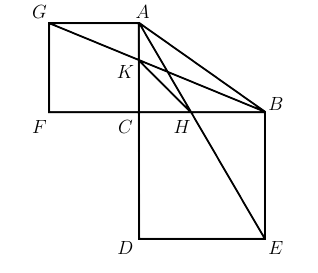
Soit $ABC$ un triangle rectangle dont l'angle droit est en $C$. Soit $BCDE$ et $ACFG$ des carrés situés à l'extérieur du triangle. De plus, le segment $AE$ croise $BC$ en $H$ et le segment $BG$ croise $AC$ en $K$. Déterminez la mesure de $\angle DKH$.
-
Solution
(publié le
6 octobre)
Il s'agit du problème 1 de l'édition 2005 de l'Olympiade mathématique australienne qui a aussi été donné dans la section Olympiad du Crux Mathematicorum [2009:146-147]. La solution proposée vient de Geoffrey Kandall, de Hamden au Connecticut, États-Unis, et a été publiée dans l'édition [2010:229].
Soit $BC = a$ et $AC = b$. Le triangle $KCB$ est semblable au triangle $GFB$ et le triangle $HCA$ semblable au triangle $EDA$. Ainsi,
$\frac{KC}{b} = \frac{a}{a+b}$ et $\frac{HC}{a} = \frac{b}{a+b}.$Conséquemment, $KC = HC = \frac{ab}{a+b}$, donc $\angle DKH = 45^\circ$.
Semaine 4
-
Problème
(publié le
22 septembre)
Trouvez toutes les paires de nombres réels $(x,y)$ tels que $$x^6 = y^4 +18,$$ $$y^6 =x^4 + 18.$$
-
Solution
(publié le
29 septembre)
Il s'agit du problème 6 du concours en équipe Lithuanien 2004 donné dans la section Olympiad du Crux Mathematicorum [2008:282-284]. La solution donnée dans l'édition [2009:298] provient de George Apostolopoulos, de Messolnghi en Grèce.
Remarquons que $x \neq 0$ et $y \neq 0$. Puisque $x^6-y^4 = 18$ et $y^6-x^4 =18$, on a
$\begin{array}{ccc} x^6-y^6 +x^4-y^4 &=& 0 \\(x^2)^3-(y^2)^3 +(x^2)^2 -(y^2)^2 & = & 0 \\(x^2-y^2)(x^4 +x^2y^2 +y^4) + (x^2-y^2)(x^2+y^2) & = & 0\\(x^2-y^2)(x^4+x^2y^2+y^4+x^2+y^2) & = & 0 \end{array}$
Par contre, $x^4+x^2y^2+y^4+x^2+y^2>0$ donc $x^2=y^2$ et $x^6-x^4-18=0$. En posant $x^2 =w$, l'équation en $x$ devient $w^3-w^2-18=0$ ou $(w-3)(w^2+2w+6)=0$. Ainsi, $w=3$, puisque $w^2+2w+6 = x^4+2x^2+6=0$ est positive pour tous les nombres réels. On sait que $x^2=w = 3$ et donc $x= \pm \sqrt{3}$. Il y a donc quatre solutions à l'équation: $(x,y) = (\pm \sqrt{3},\pm \sqrt{3}).$
Semaine 3
-
Problème
(publié le
15 septembre)
Soit $a$,$b$ et $c$ des nombres réels non nuls. Trouvez $x$, $y$ et $z$ si $$ \frac{ay+bx}{xy}=\frac{bz+cy}{yz}=\frac{cx+az}{zx}=\frac{4a^2+4b^2+4c^2}{x^2+y^2+z^2}.$$
-
Solution
(publié le
22 septembre)
Il s'agit du problème 3 du Concours mathématique de Croatie 2007 donné dans la section Skoliad du Crux Mathematicorum [2008:195-196]. La solution est de Johan Gunardi, étudiant au SMPK 4 BPK PENABUR à Jakarta en Indonésie et est apparue dans l'édition [2009:132].
On sait que $\frac{a}{x}+\frac{b}{y} = \frac{b}{y}+\frac{c}{z} = \frac{c}{z} + \frac{a}{x}$, ce qui implique que $\frac{a}{x}=\frac{b}{y}=\frac{c}{z}.$ Soit $k$ cette valeur commune. Alors $a=kx,b=ky,$ et $c=kz$. En substituant ces valeurs dans l'équation de départ, on obtient $2k =\frac{4k^2x^2+4k^2y^2+4k^2z^2}{x^2+y^2+z^2}=4k^2$ donc $k=0$ ou $k= \frac{1}{2}.$ Si $k=0$, alors $a=b=c=0$, ce qui contredit le fait que $a,b$ et $c$ sont non nuls. Si $k=\frac{1}{2}$, alors $x=2a,y=2b,$ et $z=2c$.
Semaine 2
-
Problème
(publié le
8 septembre)
Huit balles dans deux urnes
On vous donne deux urnes identiques et opaques, quatre balles blanches et quatre balles noires. Vous devez séparer les balles dans chacune des urnes (sans nécessairement en mettre autant dans chaque urne). Après avoir placé les balles, une tierce personne peut échanger les urnes afin qu'il vous soit impossible de les différencier. De quelle façon devriez-vous disposer les balles afin de maximiser la probabilité de piger une balle blanche en pigeant une balle de façon aléatoire dans une urne choisie aléatoirement?
-
Solution
(publié le
15 septembre)
Il s'agit du problème 3 du concours québécois (niveau secondaire) de février 2006 qui a été donné dans la section Skoliad du Crux Mathematicorum [2008:67-68]. La solution a été écrite par l'éditeur dans le Crux Mathematicorum [2009:8].
On met $1$ balle blanche dans une urne et toutes les autres balles dans l'autre urne. La probabilité de choisir l'urne contenant $1$ balle blanche et ensuite piger cette balle est $\frac{1}{2}\cdot 1= \frac{1}{2}$ et la probabilité de choisir l'autre urne et de piger une balle blanche est $\frac{1}{2}\cdot \frac{3}{3+4}=\frac{3}{14}.$ Ainsi, avec cette disposition des balles dans les urnes, la probabilité de piger une balle blanche est $p =\frac{1}{2}\cdot 1 + \frac{1}{2} \cdot \frac{3}{7}= \frac{5}{7}.$
Posons $p_1$ et $p_2$ les probabilités de piger une balle blanche dans chacune des deux urnes ($p_1 =1$ et $p_2 = \frac{3}{7}$ dans notre exemple précédent). La probabilité totale de piger une balle blanche est alors $p = \frac{1}{2} p_1 + \frac{1}{2} p_2 = \frac{p_1+p_2}{2}$, qui est la moyenne des valeurs $p_1$ et $p_2$. Ainsi, comme $p>\frac{5}{7}$, on doit nécessairement avoir que $p_1 > \frac{5}{7}$ ou $p_2 > \frac{5}{7}.$ Pour faire une urne avec $p_1 > \frac{5}{7}$ (sans perte de généralité), on doit avoir $(b,n) = (1,0),(2,0),(3,0) (3,1),(4,0)$ ou $(4,1),$ l'urne contenant $b$ balles blanches et $n$ balles noires. Ce sont les seules dispositions qui sont susceptibles de nous donner $p > \frac{5}{7}.$ Dans le cas de $(b,n) = (2,0),(3,0),$ ou $(4,0),$ on a $p<\frac{5}{7}$ puisque bouger une balle blanche dans la deuxième urne fait augmenter $p_2$ sans modifier la valeur de $p_1 =1.$ Finalement, on peut calculer la valeur de $p$ pour $(b,n) = (3,1)$ et $(4,1)$, ce qui nous donne $p = \frac{1}{2}$ et $p = \frac{2}{5}$, chacun d'eux étant inférieur à $\frac{5}{7}.$
La distribution expliquée initialement est donc celle qui maximise la probabilité de piger une balle blanche.
Semaine 1
-
Problème
(publié le
1 septembre)
Cette semaine, nous présentons deux problèmes d'introduction. Essayez-les! La source du problème ainsi que sa solution seront disponibles la semaine prochaine.
Problème A
Trouvez deux facteurs de $2^{48}-1$ situés entre $60$ et $70$.Problème B
Un point est choisi arbitrairement à l'intérieur d'un triangle équilatéral. À partir de ce point, on trace des perpendiculaires à chacun des côtés du triangle. Montrez que la somme des longueurs de ces perpendiculaires est égale à la longueur de la hauteur du triangle.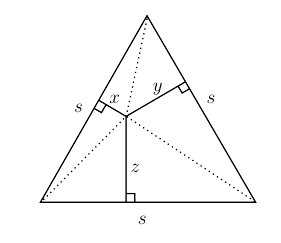
-
Solution
(publié le
8 septembre)
Problème A
Il s'agit du problème 4 de la $23^{e}$ édition du concours mathématique W. J. Blundon (2006). Il a aussi été donné dans la section Skoliad du Crux Mathematicorum [2007:321-322], avec une solution de Ruiqi Yi, étudiant au Stephen Leacock Collegiate Institute à Toronto, qui est apparue dans l'édition [2008:197]
En utilisant la formule $x^2-y^2=(x-y)(x+y)$ à plusieurs reprises, on trouve que $$2^{48}-1=(2^{24}+1)(2^{12}+1)(2^6+1)(2^6-1).$$ Puisque $2^{6}= 64$, $63$ et $65$ sont deux facteurs de $2^{48}-1$ entre $60$ et $70$.Problème B
Il s'agit du problème 8 du même concours que le précédent. La solution officielle modifiée par l'éditeur a été donnée dans l'édition [2008:198-199].
Soit $s$ la longueur des côtés du triangle, $h$ celle de la hauteur et $x,y,$ et $z$ les distances entre le point et chacun des côtés. Ainsi, $$\begin{array}{ccc} \mbox{Aire du triangle} &= &\frac{1}{2} sx + \frac{1}{2} sy + \frac{1}{2} sz \\ & = & \frac{1}{2}s(x+y+z). \end{array}$$Mais on a aussi $$\mbox{Aire du triangle} = \frac{1}{2} sh$$.
En simplifiant le $\frac{1}{2}s $ de chacune des expressions pour l'aire, on obtient $x+y+z =h$.


Pour signaler des erreurs ou des faits manquants pour cette page, veuillez communiquer avec nous au docm@smc.math.ca.
