


Next: Siddharta Sahi - To
Up: Algebraic Combinatorics, Group Representations
Previous: Alain Lascoux - Graphe
| JENNIFER MORSE, University of Pennsylvania, Philadelphia, Pennsylvania 19104
USA |
| A new basis for Macdonald polynomials |
We will present a set of multivariate symmetric polynomials,
with
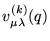 a polynomial in q with positive
integer coefficients and
a polynomial in q with positive
integer coefficients and
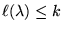 . We conjecture that
for any partition
. We conjecture that
for any partition 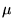 with
with
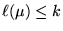 , the Hall-Littlewood
polynomials can be expanded in this basis as
, the Hall-Littlewood
polynomials can be expanded in this basis as
where
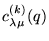 is also
is also
![$\in \bbd N[q]$](img68.gif) . The
. The
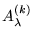 basis provides a natural mechanism to divide the
set of standard tableaux into families and is loosely related to the
atomic decomposition of Lascoux and Schützenberger. We will discuss
properties of this basis that are associated to tableaux combinatorics,
creation operators, Pieri formulas and the Macdonald polynomials.
basis provides a natural mechanism to divide the
set of standard tableaux into families and is loosely related to the
atomic decomposition of Lascoux and Schützenberger. We will discuss
properties of this basis that are associated to tableaux combinatorics,
creation operators, Pieri formulas and the Macdonald polynomials.

