Luigi Santocanale - Free -lattices1

Next: Claude Tardif - Projectivity Up: Orders, Lattices and Universal Previous: Bob Quackenbush - Duality

Luigi Santocanale - Free 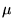$\mu$ -lattices¹

LUIGI SANTOCANALE, Département de mathématiques, Université du Québec à Montréal, Montréal, Québec H3C 3P8

Free $\mu$ -lattices²

If P is a partially ordered set and $\phi$ is an order preserving function from P to P, the least prefix-point of $\phi$ is an element $\mu$ of P such that $\phi( \mu ) \leq \mu$ and such that if $\phi(p) \leq p$ , then $\mu \leq p$ . The greatest postfix-point is defined dually.

A lattice is a $\mu$ -lattice if every unary polynomial has a least prefix-point and a greatest postfix-point. For a unary polynomial we mean a derived operator evaluated in all but one variables; operators are derived from the basic ones of lattice theory by substitution and by ``taking fix-points''. A category of $\mu$ -lattices is defined and it turns out to be a quasivariety. For a given partially ordered set P, we describe a $\mu$ -lattice J_P by means of games: we define a class J(P) whise elements are games and a preorder on it by saying that, for $G,H \in J(P)$ , $G \leq H$ if and only if a specified player has a winning strategy in a compound game [G,H]. This relation is shown to be decidable if the order of P is decidable.

By showing that J_P is free over P we give a solution to the word problem for the theory of $\mu$ -lattices.

Next: Claude Tardif - Projectivity Up: Orders, Lattices and Universal Previous: Bob Quackenbush - Duality