Kenneth Williams - Values of the Dedekind eta function at quadratic irrationalities

Next: Operator Algebras / Algèbres Up: Number Theory / Théorie Previous: Hugh Williams - Computer 5.10

Kenneth Williams - Values of the Dedekind eta function at quadratic irrationalities

KENNETH WILLIAMS, School of Mathematics and Statistics, Carleton University, Ottawa, Ontario K1S 5B6, Canada

Values of the Dedekind eta function at quadratic irrationalities

The Dedekind eta function $\eta(z)$ is defined by

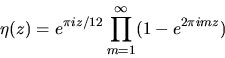
$\begin{displaymath}\eta (z) = e^{\pi i z/12} \prod^\infty_{m=1} (1-e^{2\pi imz}) \end{displaymath}$

for im (z) >0. Let d be the discriminant of an imaginary quadratic field. The value of $\bigl\vert \eta \bigl((b +\sqrt{d}/2a\bigr)\bigr\vert$ is determined for integers a, b, c satisfying

$\begin{displaymath}b^2 -4ac = d, \quad a >0, \ (a,b,c) =1. \end{displaymath}$

This is joint work with A. J. van der Poorten.