W. Georg Nowak - Large convex domains sometimes contain more lattice points than we would expect

Next: Yannis Petridis - Zeros Up: Number Theory / Théorie Previous: Kumar Murty - Zeros

W. Georg Nowak - Large convex domains sometimes contain more lattice points than we would expect

W. GEORG NOWAK, Universität für Bodenkultur, A-1180 Vienna, Austria

Large convex domains sometimes contain more lattice points than we would expect

Let as usual r(n) denote the number of ways to write $n\in{\bf N}$ as a sum of two squares. Then the quantity

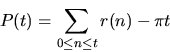
$\begin{displaymath}P(t) = \sum_{0\le n\le t} r(n) - \pi t \end{displaymath}$

(the ``lattice rest'' of an origin-centered circle of radius $\sqrt{t}$ ) is well-known to satisfy

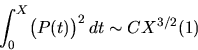
$\begin{displaymath}\int_0^X \bigl(P(t)\bigr)^2 \,dt \sim C X^{3/2} \leqno (1) \end{displaymath}$

(Cramér, Landau),

$\begin{displaymath}\liminf_{t\to\infty} {P(t) \over (t\log t)^{1/4}} < 0 \leqno (2) \end{displaymath}$

(Hardy), and

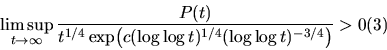
$\begin{displaymath}\limsup_{t\to\infty} {P(t) \over t^{1/4}\exp\bigl(c(\log\log t)^{1/4}(\log\log t)^{-3/4}\bigr)} > 0 \leqno (3) \end{displaymath}$

(Corrádi & Kátai). Compared to (2), (3) is not only weaker but also incapable of generalisation to more general domains, its proof being based on rather special ``arithmetic'' arguments.

The present talk addresses the corresponding problem for cubes: Let

$\begin{displaymath}r_3(n) = \char93 \{(u,v)\in{\bf Z}^2: \vert u\vert^3 + \vert v\vert^3 = n \} , \end{displaymath}$

and denote by P₃(t) the error term in the asymptotic formula for $\sum_{0\le n\le t^{3/2}}r_3(n)$ . Combining classic analytic number theory with some profound algebra and a very recent deep result of Heath-Brown [1], the authors [2] where able to show that

$\begin{displaymath}\limsup_{t\to\infty} {P_3(t) \over (t \log\log t)^{1/4}} > 0. \end{displaymath}$

This is based on the fact that the set

$\begin{displaymath}\{(m^{3/2}+n^{3/2})^{2/3} : (m,n)\in{\bf N}^2,\gcd (m,n) = 1\} \end{displaymath}$

contains a rather ``large'' set of numbers which are linearly independent over the rationals.

The corresponding general problem for r_k(n), k>3, remains open at the present state-of-art.

References

1. D. R. Heath-Brown, The density of rational points on cubic surfaces. Acta Arith. 79(1997), 17-30. 2. M. Kühleitner, W. G. Nowak, J. Schoißengeier and T. Wooley, On sums of two cubes: An $\Omega_+$ -estimate for the error term. Acta Arith. 85(1998), 179-195.

Next: Yannis Petridis - Zeros Up: Number Theory / Théorie Previous: Kumar Murty - Zeros