Next: Reg Kulperger - Empirical Up: Probability Theory / Théorie Previous: Gail Ivanoff - Set-indexed
Michael Kouritzin - Parabolic equations with random coefficients
| MICHAEL KOURITZIN, University of Alberta, Edmonton, Alberta T6G 2G1, Canada |
| Parabolic equations with random coefficients |
Questions related to the asymptotic behavior (as
![]() ) of systems of random ordinary differential equations
) of systems of random ordinary differential equations
where
A natural question that is important to filtering theory and
stochastic
control is whether these convergence results continue to hold for the
parabolic partial differential equations
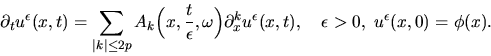
For second order parabolic equations with various technical and simplifying assumptions, earlier results indicate that laws of large numbers and fluctuation results continue to hold, provided one resorts to spaces of generalized functions for the fluctuation results. In this talk, we will discuss general convergence and rate of convergence results for
Next: Reg Kulperger - Empirical Up: Probability Theory / Théorie Previous: Gail Ivanoff - Set-indexed

