John Phillips - Spectral flow and index in bounded and unbounded -summable Fredholm modules: integral formulas

Next: Jack Spielberg - A Up: Operator Algebras / Algèbres Previous: Alexandru Nica - Some

John Phillips - Spectral flow and index in bounded and unbounded 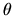$\theta$ -summable Fredholm modules: integral formulas

JOHN PHILLIPS, Department of Mathematics and Statistics, University of Victoria, Victoria, British Columbia V8W 3P4, Canada

Spectral flow and index in bounded and unbounded $\theta$ -summable Fredholm modules: integral formulas

In joint work with Alan Carey, we study $\theta$ -summable Fredholm modules (H,D₀) for Banach ${\ast}$ -algebras, A, and integral formulas for the pairing of (H,D₀) with K₁(A). In particular, if (H, D₀) is $\theta$ -summable (in Connes' original sense that $\textrm{Tr}(e^{-t D_0^2})<\infty$ for all t>0) then we prove that if u is a unitary in A¹ with [u,D₀] bounded and $P=\chi_{[0,\infty )}(D_0)$ , then

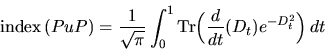
$\begin{displaymath}{\rm index}\,(PuP)={1\over {\sqrt{\pi}}} \int_0^1\textrm{Tr}\Bigl({d\over { dt}} (D_t) e^{-D_t^2}\Bigr)\,dt \end{displaymath}$

where $D_t=D_0+t(uD_0u^{\ast}-D_0)$ is the straight line path from D₀ to $uD_0u^{\ast}$ . This is the pairing of [u] in K₁(A) with [D₀] in K¹(A) and can also be interpreted as the spectral flow of the path $\{D_t\}$ . A proof of this formula was first outlined by Ezra Getzler.

Our proof is quite different from the one indicated by Getzler. Our method is able to handle Connes' new notion of $\theta$ -summability (which we dub weak- $\theta$ -summability) i.e., $\textrm{Tr}(e^{-t D_0^2})<\infty$ for some t>0. We can also handle the various bounded notions of $\theta$ -summability (indeed, our method is based on this). Finally our method simultaneously deals with the $\hbox{II}_{\infty}$ -version of all these results.

Roughly speaking, our proofs involve three steps. First, given (H ,D₀) we make a careful analytic study of the map $D\mapsto F_D:=D(1+D^2 )^{-{1\over 2}}$ defined for D in $D_0+{\cal B}(H)_{\textrm{sa}}$ . The pair (H,F_D₀) is a pre-Fredholm module for Awhich is $\theta$ -summable (in a restricted sense) and the F_D vary in a certain affine space of bounded self-adjoint operators, $F_{D_0}+{\cal L}_{\textrm{sa}}$ . We show that this map

$\begin{displaymath}D\mapsto F_D\colon D_0+{\cal B}(H)_{\textrm{sa}}\rightarrow F_{D_0}+{\cal L}_{\textrm{sa}} \end{displaymath}$

is suitably smooth. Second, we study the various notions of bounded $\theta$ -summability that arise in this context. In particular, one of our results shows that if (H,F₀) is a pre-Fredholm module which is $\theta$ -summable for A in the strongest sense, then for F in $F_0+{\cal L}_{\textrm{sa}}$ and X in ${\cal L}_{\textrm{sa}}$ (the tangent space to $F_0+{\cal L}_{\textrm{sa}}$ at F), Tr(X e^{-|1-F²|^-1}) is a closed (and exact) 1-form on the manifold, $F_0+{\cal L}_{\textrm{sa}}$ . The idea to use these differential-geometric notions in this context goes back to I.M. Singer and was also used by Getzler in his proof. The point here is that now the integral

$\begin{displaymath}\int_0^1\textrm{Tr}\Bigl({d\over {dt}}(F_t)e^{-\vert 1-F_t^2\vert^{-1}}\Bigr)\,dt \end{displaymath}$

is seen to be independent of path in the space, $F_0+{\cal L}_{\textrm{sa}}$ . Third, we can now reduce to the case of genuine (bounded, $\theta$ -summable) Fredholm modules (H,F₀) (i.e., F₀²=1), and paths $F_t=F_0+t(uF_0u^{\ast}-F_0)$ . In this setting, P=2F₀-1and the formula

$\begin{displaymath}\textrm{Index}(PuP)={1\over C} \int_0^1\textrm{Tr}\Bigl({d\over { dt}}(F_t)e^{-\vert 1-F_t^2\vert^{-1}}\Bigr)\,dt \end{displaymath}$

is still not a triviality.

As mentioned above, our results are proved in such a way that the type $\hbox{II}_{\infty}$ case is included at all stages.

Next: Jack Spielberg - A Up: Operator Algebras / Algèbres Previous: Alexandru Nica - Some