Next: Manfred Kolster - Higher Up: Number Theory / Théorie Previous: James Huard - An
Hershey Kisilevsky - Rank of E(K) for cyclic cubic extensions 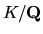
| HERSHEY KISILEVSKY, Concordia University, Montreal, Quebec H3G 1M8, Canada |
| Rank of E(K) for cyclic cubic extensions |
For an elliptic curve, E, defined over the rational field, we consider
the rank of E(K) for cyclic cubic extensions ![]() .
.

