James Huard - An arithmetic reciprocity relation of Liouville type and applications

Next: Hershey Kisilevsky - Rank Up: Number Theory / Théorie Previous: C. Greither - On

James Huard - An arithmetic reciprocity relation of Liouville type and applications

JAMES HUARD, Department of Mathematics, Canisius College, Buffalo, New York 14208, USA

An arithmetic reciprocity relation of Liouville type and applications

Let n be a positive integer and let $f\colon {\bf Z}\rightarrow {\bf C}$ be an even function. Liouville gave the identity
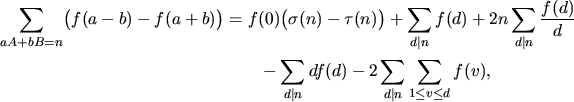
$\begin{align*}\sum_{aA + bB = n} \bigl( f(a-b) -f (a+b)\bigr) &\null= f(0) \bigl... ...sum_{d\vert n} df(d) - 2\sum_{d\vert n} \sum_{1\leq v \leq d} f(v), \end{align*}$
where the sum on the left hand side is taken over all positive integers a, A, b, B satisfying aA + bB =n. Some generalizations of this identity will be presented and applications will be made to the determination of such sums as

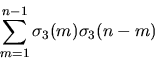
$\begin{displaymath}\sum^{n-1}_{m=1} \sigma_3 (m)\sigma_3 (n-m) \end{displaymath}$

and to the representation of n by certain positive quaternary quadratic forms. The proofs of these results require elementary methods. This is a joint work with Z. Ou, B. K. Spearman, and K. S. Williams.

Next: Hershey Kisilevsky - Rank Up: Number Theory / Théorie Previous: C. Greither - On