Next: Jack Spielberg - A Up: Operator Algebras / Algèbres Previous: Alexandru Nica - Some
John Phillips - Spectral flow and index in bounded and unbounded
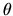 -summable Fredholm modules: integral formulas
-summable Fredholm modules: integral formulas
| JOHN PHILLIPS, Department of Mathematics and Statistics, University of Victoria, Victoria, British Columbia V8W 3P4, Canada |
| Spectral flow and index in bounded and unbounded
|
In joint work with Alan Carey, we study ![]() -summable Fredholm
modules (H,D0) for Banach
-summable Fredholm
modules (H,D0) for Banach ![]() -algebras, A, and integral
formulas for the pairing of (H,D0) with K1(A). In particular, if
(H, D0) is
-algebras, A, and integral
formulas for the pairing of (H,D0) with K1(A). In particular, if
(H, D0) is ![]() -summable (in Connes' original sense that
-summable (in Connes' original sense that
![]() for all t>0) then we prove that if u is
a unitary in A1 with [u,D0] bounded and
for all t>0) then we prove that if u is
a unitary in A1 with [u,D0] bounded and
![]() , then
, then
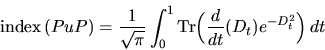
where
Our proof is quite different from the one indicated by Getzler. Our
method is able to handle Connes' new notion of ![]() -summability
(which we dub
weak-
-summability
(which we dub
weak-![]() -summability) i.e.,
-summability) i.e.,
![]() for some t>0. We can also handle the
various bounded notions of
for some t>0. We can also handle the
various bounded notions of ![]() -summability (indeed, our method is
based on this). Finally our method simultaneously deals with the
-summability (indeed, our method is
based on this). Finally our method simultaneously deals with the
![]() -version of all these results.
-version of all these results.
Roughly speaking, our proofs involve three steps. First, given (H
,D0) we make a careful analytic study of the map
![]() defined for D in
defined for D in
![]() . The pair
(H,FD0) is a pre-Fredholm module for Awhich is
. The pair
(H,FD0) is a pre-Fredholm module for Awhich is ![]() -summable (in a restricted sense) and the FD vary
in a certain affine space of bounded self-adjoint operators,
-summable (in a restricted sense) and the FD vary
in a certain affine space of bounded self-adjoint operators,
![]() . We show that this map
. We show that this map
is suitably smooth. Second, we study the various notions of bounded
is seen to be independent of path in the space,
is still not a triviality.
As mentioned above, our results are proved in such a way that the
type
![]() case is included at all stages.
case is included at all stages.
Next: Jack Spielberg - A Up: Operator Algebras / Algèbres Previous: Alexandru Nica - Some

