Felix Lazebnik - On a class of algebraically defined graphs

Next: Laszlo Székely - Some Up: Extremal Combinatorics / Combinatoire Previous: Penny Haxell - Integer

Felix Lazebnik - On a class of algebraically defined graphs

FELIX LAZEBNIK, Department of Mathematical Sciences, University of Delaware, Newark, Delaware 19716, USA

On a class of algebraically defined graphs

Let Fⁿ denote be the n-dimensional vector space over a field F. For $n\ge 2$ and each $i= 1,2,\ldots, n-1$ , let $f_i\colon F^{2i}\to F$ be a function of 2i variables. We consider a bipartite graph whose vertex partitions P and L are copies of Fⁿ with $p = (p_1,p_2,\ldots, p_n)\in P$ and $l = (l_1,l_2,\ldots, l_n)\in L$ being joined by an edge if and only if the following n-1 equalities are satisfied:

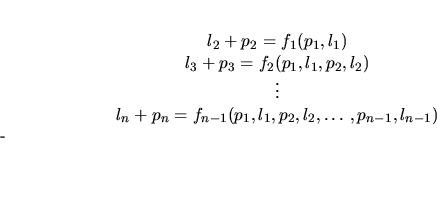
$\begin{displaymath}\displaylines{ l_2 + p_2 = f_1(p_1,l_1)\cr l_3 + p_3 = f_2(p_... ... p_n = f_{n-1}(p_1,l_1, p_2,l_2, \ldots, p_{n-1},l_{n-1})\cr } \end{displaymath}$

For particular fields F and particular functions f_i's, the families of graphs defined this way (or slightly modified) possesses many remarkable properties. They are concerned with forbidden cycles, girth, graph homomorphism, eigenvalues, and edge-decompositions of complete graphs and complete bipartite graphs. In this talk we survey some known and some new results on such graphs based on the work of A. J. Woldar and the speaker.

Next: Laszlo Székely - Some Up: Extremal Combinatorics / Combinatoire Previous: Penny Haxell - Integer