Ludwig Danzer and Gerrit van Ophuysen - A species of planar triangular tilings with inflation factor

Next: Robert Dawson - What Up: Discrete Geometry / Géométrie Previous: Balázs Csikós - Some

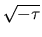
Ludwig Danzer and Gerrit van Ophuysen - A species of planar triangular tilings with inflation factor $\sqrt{-\tau}$

LUDWIG DANZER AND GERRIT VAN OPHUYSEN, Universität Dortmund, Facherbereich Mathematik, Lehrstuhl II, 44221 Dortmund, Germany

A species of planar triangular tilings with inflation factor $\sqrt{-\tau}$

Consider the set ${\cal F}= \{A,X\}$ of two right triangles in $\bbd E^2$ with sides having squared lengths 1, $\tau$ , $1+ \tau$ and $\tau$ , $\tau^2$ , $\tau+\tau^2$ respectively. These can be glued together (in only one way) to form a third right triangle $X \mathop{\dot\cup} A$ with sides of squared length $1+ \tau$ , $\tau+\tau^2$ , $(q + \tau)^2$ . We then consider the inflation rule infl(A):=X, $\textrm{infl} (X) : = X \mathop{\dot\cup}A$ . Interpreting $\bbd E^2$ as $\bbd C$ the inflation factor $\eta$ becomes $i \sqrt{\tau}$ which is a complex Pisot-number. The species ${\cal S}({\cal F}, \textrm{infl})$ of all global ${\cal F}$ -tilings created by $\mbox{infl}$ has a unique deflation (`` infl^-1'') and hence is aperiodic. 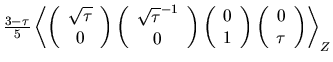The set of all vertices can be shown to be a ``model set'' (Robert Moody), so the Fourier-transformation of the autocorrelation function is ``pure point'' with the Bragg-peaks located on the $\bbd Z$ -module $\frac {3-\tau}{5} \left\langle \left( \begin{array}{c} \sqrt{\tau} \\ 0 \end{ar... ...} \right) \left( \begin{array}{c}0 \\ \tau \end{array} \right) \right\rangle _Z$ .

With ${\cal F}_c := \{ A, B, C, X, Y, Z \}$ , where B and C are congruent to A, while Y and Z are congruent to X, but all differently coloured, and

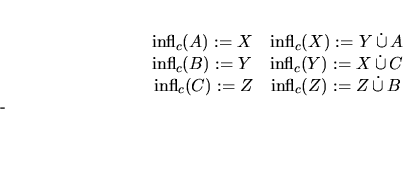
$\begin{displaymath}\displaylines{ \textrm{infl}_c(A):= X \quad \textrm{infl}_c(X... ...c(C):= Z \quad \textrm{infl}_c(Z) := Z \mathop{\dot\cup}B\cr } \end{displaymath}$

we receive the species ${\cal S}({\cal F}_{c}, \textrm{infl}_{c})$ of coloured tilings. In contrast to ${\cal S}({\cal F}, \textrm{infl})$ the coloured species can also be defined by a perfect local matching rule. In fact the 42 coloured vertex- stars may serve as an atlas.

Next: Robert Dawson - What Up: Discrete Geometry / Géométrie Previous: Balázs Csikós - Some