Andrei V. Gagarin - Characterizations of -polar graphs by forbidden induced subgraphs

Next: Malcolm Harper - A Up: Graduate Student Seminar / Previous: Shaun Fallat - Multiplicative

Andrei V. Gagarin - Characterizations of 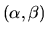$(\alpha, \beta)$ -polar graphs by forbidden induced subgraphs

ANDREI V. GAGARIN, Department of Mathematics, University of Manitoba, Winnipeg, Manitoba R3T 2N2, Canada

Characterizations of $(\alpha, \beta)$ -polar graphs by forbidden induced subgraphs

Let $\alpha$ and $\beta$ be positive integers or infinity. A graph Gis called $(\alpha, \beta)$ -polar if there is a partition of its vertex set $V(G)=A\cup B$ , $A \cap B=\varnothing$ , such that the induced subgraph G(B) is a union of disjoint cliques of order at most $\beta$ and G(A) is the complement to a union of disjoint cliques of order at most $\alpha$ .

In this talk, we will consider the problem of characterizing $(\alpha, \beta)$ -polar classes in terms of a finite list of forbidden induced subgraphs.