Victor Alexandrov - Sufficient conditions for the extendability of an N-th order flex of polyhedra

Next: Valery Alexeev - Families Up: Discrete Geometry / Géométrie Previous: Discrete Geometry / Géométrie

Victor Alexandrov - Sufficient conditions for the extendability of an N-th order flex of polyhedra

VICTOR ALEXANDROV, Sobolev Institute of Mathematics, Novosibirsk, 630090 Russia

Sufficient conditions for the extendability of an N-th order flex of polyhedra

A very long-standing (and still open) problem is to prove that a smooth compact surface in Euclidean 3-space is rigid. Classical attempts to solve this problem were based on the notion of an infinitesimal flex. Since a counterexample was constructed by R. Connelly in the class of polyhedral surfaces, particular attention was given to studying infinitesimal flexes of polyhedra.

We give a new approach to describing a high order flex of polyhedra. The main results provide some sufficient conditions under which an infinitesimal flex of a polyhedron can be extended to an authentic flex. We discuss also results of computer experiments demonstrating that one set of our sufficient conditions is fulfilled for the Bricard octahedra.

More precisely, let Q be a closed polyhedron with v vertexes, eedges and triangular faces. A special bilinear map $B\colon\bbd R^{3v} \times \bbd R^{3v} \to \bbd R^{e}$ is constructed in such a way that the vector

$\begin{displaymath}X_0+tX_1+\cdots +t^kX_k \quad (X_j\in\Bbb R^{3v}, j=0,1,\dots ,k)\leqno(1) \end{displaymath}$

is the k-th order infinitesimal flex of the polyhedron X₀=Q if and only if the equation

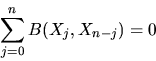
$\begin{displaymath}\sum_{j=0}^{n} B(X_j,X_{n-j})=0 \end{displaymath}$

holds for each $1\leq n\leq k$ . Put A₀X=B(X, X₀)+ B(X₀ ,X). Suppose an infinitesimal flex $X_0+tX_1+\cdots +t^nX_n$ of the polyhedron Q is given. To extend this flex into a higher order one, it is necessary to solve the linear equation

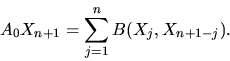
$\begin{displaymath}A_0X_{n+1} =\sum_{j=1}^{n} B(X_j,X_{n+1-j}). \end{displaymath}$

The following sufficient condition for algorithmic verification of the flexibility of polyhedra is proven:

Theorem. Let a polyhedron Q=X₀ has an infinitesimal flex $X_0+tX_1+\cdots +t^nX_n$ and let $L_n\subset\bbd R^{3v}$ be the linear span of the vectors $X_0, X_1, \dots , X_n$ . Suppose the equation A₀X=-B(X_i, X_j)-B(X_j,X_i) has a solution $X\in L_n$ for all $1\leq i\leq n$ , $1\leq j\leq n$ . Then Q is flexible.

Computer experiments show that the conditions of the Theorem are fulfilled with n=5 for Bricard's octahedron of the second type.

Next: Valery Alexeev - Families Up: Discrete Geometry / Géométrie Previous: Discrete Geometry / Géométrie