Stewart Priddy - Decomposing products of classifying spaces

Next: Charles Rezk - A Up: 2) Homotopy Theory / Théorie Previous: Joseph Neisendorfer - James-Hopf

Stewart Priddy - Decomposing products of classifying spaces

STEWART PRIDDY, Department of Mathematics, Northwestern University, Evanston, Illinois 60208, USA

Decomposing products of classifying spaces

Let $G = H \times K$ be the product of two finite groups. The problem of determining the stable type of the classifying space $BG=BH \times BK$ , localized at a prime p, is often quite difficult due to the complicated nature of the subgroups of G which generally do not relate well to those of H and K. Of course, the usual stable decomposition of a product of spaces $X \times Y \cong X \vee Y \vee (X \wedge Y)$ gives a decomposition of BG but these summands may be decomposable, even in elementary cases such as $B({\bf Z}/2\times {\bf Z}/2)$ . In some situations however, the stable type of BG is closely related to that of BH and BK. We say BG is smash decomposable if the indecomposable summands of BG₊ are given by simply smashing together those of BH₊ and BK₊, that is, a complete splitting for BG₊ localized at p has the form

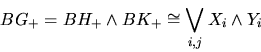
$\begin{displaymath}BG_{+}= BH_{+}\wedge BK_{+} \cong \bigvee_{i,j} X_i \wedge Y_i \end{displaymath}$

where $BH_{+}\cong \bigvee_i X_i$ , $BK_{+} \cong \bigvee_j Y_j$ are complete splittings into indecomposable summands. Here BG₊ is BG with a disjoint basepoint. This is convenient for converting from Cartesian products to smash products since $(X \times Y)_{+}= X_{+}\wedge Y_{+}$ . Further $BG_{+} = BG \vee S^0$ . Thus BG is smash decomposable when the $X_i\wedge Y_j$ are indecomposable. In this talk we study groups for which BG is smash decomposable.

(Joint work with John Martino and Jason Douma)

Next: Charles Rezk - A Up: 2) Homotopy Theory / Théorie Previous: Joseph Neisendorfer - James-Hopf