Susan Niefield - Monoidal (bi)categories, bimodules, and adjunctions

Next: Robert Paré - Functorial Up: Category Theory / Théorie Previous: Michael Makkai - Weak

Susan Niefield - Monoidal (bi)categories, bimodules, and adjunctions

	SUSAN NIEFIELD, Union College, Schenectady, New York 12308, USA
	Monoidal (bi)categories, bimodules, and adjunctions

In this joint work with Richard Wood, we consider variations of the following earlier result of the speaker. If $\cal V$ is a monoidal category with coequalizers preserved by $\otimes$ , then there is an adjoint pair

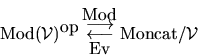
$\begin{displaymath} \textrm{Mod}({\cal V})^{\textrm{op}} \mathop{\mathop{\longle... ...\longrightarrow}\limits^{\textrm{Mod}}}\textrm{Moncat}/{\cal V}\end{displaymath}$

where $\textrm{Mod}$ takes a $\cal V$ -monoid M to the category of M-M-bimodules and $\textrm{Ev}$ takes a monoidal functor $p\colon {\cal W} \to {\cal V}$ to the $\cal V$ -monoid pI.

In each case, we consider a ``module'' functor which takes values in a category of monoidal categories with a suitable choice of morphisms. First, we replace $\textrm{Mon}({\cal V})$ by $\cal V$ -cat and $\textrm{Moncat}/{\cal V}$ by monoidal categories over certain categories of matrices in $\cal V$ . Next, we assume $\cal V$ is symmetric and obtain an adjunction between commutative $\cal V$ -monoids and monoidal $\cal V$ -categories. Finally, we generalize this to an adjunction between braided monoidal $\cal V$ -categories and monoidal $\cal V$ -bicategories.

eo@camel.math.ca