Semaine 9

• Problème (publié le 1 novembre)

  Déterminez tous les polynômes $f(x)=x^n+a_{1}x^{n-1}+a_2x^{n-2}+...+a_{n-1}x+a_n$ avec les propriétés suivantes :

  1. tous les coefficients $a_1,..,a_{n}$ appartiennent à l'ensemble $\{ -1,1\}$;
  2. toutes les solutions à l'équation $f(x)=0$ sont réelles.

• Solution (publié le 8 novembre)

  Il s'agit du problème 5 de la quatrième Olympiade mathématique d'Irlande (1991), apparu dans l'édition [1993:192-193] du Crux Mathematicorum. On présente la solution de Michael Selby, parue dans l'édition [1995:12-13].

  Soit $r_1,r_2,..,r_n$ les racines du polynôme. Alors \begin{align} r_1+r_2+...+r_n &= -a_{1} \cr r_1r_2+r_1r_3+...+r_{n-1}r_n &= a_{2} \cr r_1r_2...r_n &= (-1)^na_n \,. \end{align}

  On trouve alors \begin{align} r_1^2+r_2^2+..+r_n^2 &= \left(r_1+...+r_n\right)^2-2 \left(r_1r_2+r_1r_3+...+r_{n-1}r_n \right) \cr &= 1-2a_{2} \,. \end{align}

  Ceci implique que, en autant que $n \geq 2$, nous avons $1-2a_2 \geq 0$ et donc que $a_2=-1$.

  Par l'inégalité arithmético-géométrique, \begin{align} \frac{r_1^2+...+r_n^2}{n} &\geq \sqrt[n]{r_1^2r_2^2...r_n^2} \cr &= \sqrt[n]{ \left( (-1)^na_n \right)^2}=1 \end{align} avec égalité si et seulement si $r_1^2=r_2^2=...=r_n^2=1$.

  Ainsi, \[ 1-2a_2 \geq n \,, \] avec égalité si et seulement si $r_1^2=r_2^2=...=r_n^2=1$.

  Il est donc nécessaire que $n \leq 3$.

  Cas 1 : $n=1$. On voit directement que $X+1$ et $X-1$ sont des solutions.

  Cas 2 : $n=2$. On doit avoir $a_2=-1$. Les deux polynômes possibles sont donc $X^2-X-1$ et $X^2+X-1$. Ce sont tous deux des solutions.

  Cas 3 : $n=3$. On doit avoir $a_2=-1$ et égalité dans l'inégalité arithmético-géométrique, donc $r_j \in \{ \pm 1 \}$. De plus, puisque $r_1r_2+r_1r_3+r_2r_3=-1$, il n'est pas possible que toutes les racines aient le même signe. Ceci nous mène à deux polynômes possibles : \begin{align} (X-1)^2(X+1) &= X^3-X^2-X+1 \cr (X-1)(X+1)^2 &= X^3+X^2-X-1 \,. \end{align}

  Réponse : Il y a 6 polynômes qui satisfont les conditions : \[ X-1 \,;\, X+1 \,;\, X^2-X-1 \,;\, X^2+X-1 \,;\, X^3-X^2-X+1 \mbox{ et } X^3+X^2-X-1 \,. \]

Semaine 8

• Problème (publié le 25 octobre)

  On découpe un triangle équilatéral $AXY$ à partir d'un rectangle $ABCD$ de façon à ce que le sommet $X$ soit sur le côté $BC$ et que le sommet $Y$ soit sur le côté $CD$. Une fois ce triangle découpé, il reste trois triangles rectangles. Montrez que la somme des aires de deux de ces trois triangles est égale à l'aire du troisième.

  

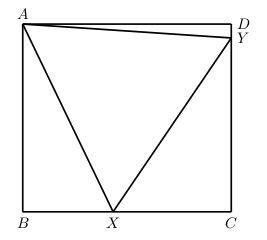
• Solution (publié le 1 novembre)

  Il s'agit du problème 2 de l'Olympiade nationale Hongroise de 1987,aussi apparu dans le Crux Mathematicorum [1989:100-101]. La solution présentée ici est celle de Michael Selby et D.J. Smeenk, parue dans l'édition [1991:68-69].

  Premièrement, on peut remarquer que cette construction n'est pas possible pour tous les rectangles. Si le rectangle a des côtés de longueur $a \leq b$, alors une condition nécessaire serait que $a \geq \frac{\sqrt{3}}{2}b$.

  Étant donné qu'il est possible de le faire, on pose $s$ pour la longueur du côté du triangle équilatéral. On affirme que \[ [XYC]=[ADY]+[ABX] \,, \] où $[T]$ signifie l'aire du triangle $T$. Utilisons $\theta_1$ et $\theta_2$ pour décrire respectivement $\angle BAX$ et $\angle DAY$.

  

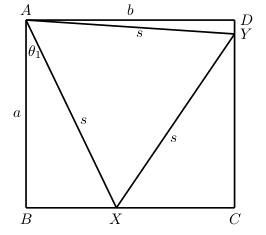
  Ainsi, \begin{align} [ABX] &= \frac{1}{2} AB \cdot BX \cr &= \frac{1}{2} s \cos(\theta_1) s \sin(\theta_1) \cr &= \frac{1}{2} s^2 \cos(\theta_1) \sin(\theta_1) \cr &= \frac{1}{4} s^2 \sin(2 \theta_1) \,, \end{align} et de la même façon \[ [ADY] =\frac{1}{4} s^2 \sin(2 \theta_2) \,. \]

  Ainsi, \begin{align} [ADY] &= \frac{1}{4} s^2 \sin(2 \theta_2) \cr &= \frac{1}{4} s^2 \sin\left(2 (30^\circ -\theta_1)\right) \cr &= \frac{1}{4} s^2 \sin\left(60^\circ -2\theta_1\right) \cr &= \frac{1}{4} s^2 \left( \frac{\sqrt{3}}{2} \cos(2\theta_1) -\frac{1}{2} \sin(2\theta_1) \right) \cr &= \left(\frac{\sqrt{3}}{8} s^2 \cos(2\theta_1) \right) -\left( \frac{1}{8} s^2 \sin(2\theta_1) \right) \,. \end{align}

  Ceci nous montre que \[ [ADY]+[ABX]= \frac{\sqrt{3}}{8} s^2 \cos(2\theta_1) +\frac{1}{8} s^2 \sin(2\theta_1) \,. \]

  Maintenant, pour $XCY$, l'angle $\angle CXY= 30^\circ+\theta_1$. Donc \begin{align} [CXY] &= \frac{1}{2} CX \cdot CY \cr &= \frac{1}{2} s^2 \sin(30^\circ+\theta_1) \cos(30^\circ+\theta_1) \cr &= \frac{1}{4} s^2 \sin(60^\circ+2 \theta_1) \cr &= \frac{\sqrt{3}}{8} s^2 \cos(2\theta_1) +\frac{1}{8} s^2\sin(2\theta_1) \cr &= [ADY]+[ABX] \,. \end{align}

Semaine 7

• Problème (publié le 18 octobre)

  $ABC$ est un triangle pour lequel $AB=AC$ et dont $\angle BAC=20^\circ$. Sur le côté $AC$, on choisit un point $D$ tel que $AD=BC$. Déterminez la mesure de l'angle $\angle CDB$.

  

• Solution (publié le 25 octobre)

  Il s'agit d'un de mes problèmes de géométrie préférés et celui-ci possède une très jolie solution. Malheureusement, la source de la question et de la solution ont été perdus.

  Sur le côté $AD$, on construit un triangle équilatéral extérieur à $ABC$ qu'on nomme $ADE$. Relions $E$ à $B$.

  

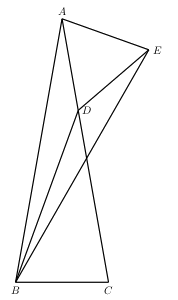
  Maintenant, par CAC, les triangles $ABC$ et $BAE$ sont congrus. Plus précisément, \[ AB=AC \,;\, \angle ABC=80^\circ =\angle BAE \,;\, BC=AE \,. \]

  Ceci implique que le triangle $BAE$ est isocèle et donc $AB=BE$.

  Ainsi, par CCC, les triangles $ADB$ et $EDB$ sont congrus. Plus précisément, \[ AD=ED \,;\, DB=DB \,;\, AB=EB \,. \] Ceci implique que $\angle ADB=\angle EDB$.

  Puisque \[ \angle ADB+\angle EDB+60^\circ =360^\circ \] on obtient \[ \angle ADB =150^\circ \,. \] et donc \[ \angle CDB =30^\circ \,. \]

Semaine 6

• Problème (publié le 11 octobre)

  Trouvez tous les nombres entiers positifs $n$ pour lesquels \[ n(n+1)(n+2)(n+3) \] a exactement 3 diviseurs premiers.

• Solution (publié le 18 octobre)

  Il s'agit du problème 5 de la ronde finale de la 30^e Olympiade mathématique d'Espagne. Celui-ci est apparu dans l'édition [1998:69-70] du Crux Mathematicorum. La solution présentée est une légère modification de celle d'Edward T.H. Wang, donnée dans l'édition [1999:203-204].

  On va montrer que les seuls entiers satisfaisant la condition sont $n=2,3$ et $6$.

  Soit $P(n)=n(n+1)(n+2)(n+3)$. Alors $P(1)=2^3 \cdot 3$ et donc $n=1$ n'est pas une solution. On suppose maintenant que $n \geq 2$.

  Remarquons premièrement que pour tout $k \in \mathbb{N},$ $(k,k+1)=(2k-1,2k+1)=1$.

  Considérons maintenant deux possibilités:

  Cas 1: $n$ est impair. Dans ce cas, les nombres $n, n+1, n+2$ sont relativement premiers deux à deux. Pour satisfaire la condition, ils doivent donc être des puissances de nombres premiers.

  Puisque $n+1$ est pair, on doit avoir que \[ n=p^a \,;\, n+1=2^b \, \mbox{ and } \, n+2=q^c \] où $a, b, c, p, q \in \mathbb N$ dont $p$ et $q$ sont des premiers impairs distincts.

  Remarquons maintenant que $n+3=2^{b}+2=2(2^{b-1}+1)$ où $b \geq 2$. Puisque les seuls diviseurs premiers possibles de $n+3$ sont $2, p$ et $q$ et que $(n+2,n+3)=1,$ il est nécessaire que \[ 2^{b-1}+1=p^d \,, \] où $d \geq 1$.

  Ainsi, \[ 2p^d=n+3=p^a+3 \,. \] Ceci montre que $p|3$ et donc que $p=3$. En divisant par $3$, on obtient \[ 2 \cdot 3^{d-1}=3^{a-1}+1 \,. \]

  Il est impossible que $d-1>0$ et $a-1>0$ puisque dans ce cas on aurait que $3|1$. Donc $d-1$ ou $a-1$ doit être $0$ et on en déduit ensuite que l'autre doit aussi être nul.

  Ceci nous montre que $a=1$ et donc que $n=3$.

  On a ainsi montré que la seule solution possible pour $n$ impair est $n=3$ et il est facile de vérifier qu'il s'agit bel et bien d'une solution.

  Cas 2: $n$ est pair. Dans ce cas, on a $(n+1,n+2)=(n+1,n+3)=(n+2,n+3)=1$. Par le même argument que dans le cas 1, on obtient l'équation \[ n+1=p^a \,;\, n+2=2^b \, \mbox{ and } \, n+3=q^c \] où $a, b, c, p, q \in \mathbb N$ dont $p,q$ sont des nombres premiers impairs distincts.

  On a ensuite que \[ n=2^b-2=2(2^{b-1}-1) \,. \]

  Ainsi $n\geq 2$ et donc $b \geq 2$.

  Si $b=2$, on a $n=2$ qui est une solution.

  Autrement, si $b \geq 3$, alors $2^{b-1}-1$ est un nombre impair supérieur ou égal à $3$. Les seuls nombres premiers qui peuvent diviser $n$ sont $2,p,q$ et comme $(n, p^a)=1$ et $2^{b-1}-1$ sont impair, on doit avoir \[ 2^{b-1}-1=q^d \,, \] où $d \geq 1$.

  Conséquemment, \[ 2q^d=n=q^c-3 \,. \] Ceci nous montre que $q|3$ et donc que $q=3$. En divisant par $3$, on obtient \[ 2 \cdot 3^{d-1}=3^{c-1}-1 \,. \] On doit avoir $d-1 \leq c-1$ et donc que $3^{d-1} |1$. Ceci implique que $d=1$ et donc \[ n=2 \cdot 3=6 \,. \]

  Il est facile de montrer que $n=6$ est réellement une solution.

  En conclusion, $n(n+1)(n+2)(n+3)$ a exactement 3 diviseurs premiers si et seulement si $n \in \{2,3,6\}$.

Semaine 5

• Problème (publié le 4 octobre)

  Cette semaine, on s'intéresse à une équation fonctionnelle.

  Trouvez toutes les fonctions $f : \mathbb{N}^* \to \mathbb{N}^*$ telles que \[ f\left(f(m)+f(n) \right) = m+n \,;\, \forall m,n \in \mathbb{N}^* \,, \] où $\mathbb{N}^*$ désigne l'ensemble $\{1,2,3,...\}$ des entiers positifs.

• Solution (publié le 11 octobre)

  C'était le problème 4 de la 44^e Olympiade mathématique de Lithuanie, aussi apparu dans l'édition [1998:196-197] du Crux Mathematicorum. La solution présentée est celle de Pierre Bornsztein et est apparue dans l'édition [1999:334-335].

  Pour $m,n \in \mathbb{N}^*$, d'après \[ f\left(f(m)+f(n) \right) = m+n \tag{1} \] \[ f\left(f(m)+f(n) \right)+f\left(f(m)+f(n) \right) =2( m+n) \]

  Donc \begin{align} f\left[ f\left(f(m)+f(n) \right)+f\left(f(m)+f(n) \right) \right] & = f(m)+f(n)+f(m)+f(n) \cr & = 2\left( f(m)+f(n) \right) \end{align} et \[ f\left[ f\left(f(m)+f(n) \right)+f\left(f(m)+f(n) \right) \right] = f(2m+2n) \,. \]

  Ainsi, \[ f(2m+2n)=2\left( f(m)+f(n) \right) \,. \tag{2} \]

  Pour $m=n$, $4f(n)=f(4n)$.

  Pour $m=2p+1, n=2p-1$ \[ 2f(2p+1)+2f(2p-1)=f(8p)=4f(2p) \] d'où $p \geq 1$, \[ f(2p+1)=2f(2p)-f(2p-1) \,. \tag{3} \]

  De même pour $m=2p+2, n=2p-2, (p \geq 2)$ on obtient \[ f(2p+2)=2f(2p)-f(2p-2) \,. \tag{4} \]

  On pose $f(1)=a, f(2)=b$.

  En utilisant $(3)$ et $(4)$ on trouve \begin{align} f(3) &= 2b-a \cr f(4) &= f(4 \cdot 1)=4f(1)=4a \cr f(5) &= 9a-2b \cr f(6) &= 8a-b \end{align}

  Mais pour $m=2,n=1$, $(2)$ conduit à \[ f(6)=2f(2)+2f(1)=2a+2b \,. \]

  Donc $8a-b=2a+2b,$ c.à.d. $b=2a$. On en déduit que pour $n \in \{ 1, 2, 3, 4, 5, 6 \}, $ \[ f(n)=an \,. \]

  Une récurrence immédiate en utilisant $(3)$ et $(4)$ permet d'obtenir: \[ f(n)=an, \, \mbox{ pour tout } n \in \mathbb{N}^*. \]

  Alors dans $(1)$, pour tout $m,n \in \mathbb{N}^*$ \[ m+n=f\left(f(m)+f(n) \right)=a(f(m)+f(n))=a^2(m+n) \,, \] d'óu $a=1$ et \[ f(n)=n \, \mbox{ pour tout } n \in \mathbb{N}^* \,. \]

  Réciproquement, $f(n)=n$ convient.

Semaine 4

• Problème (publié le 27 septembre)

  Cette semaine, on s'intéresse à un problème de cercle inscrit.

  Soit $ABC$ un triangle équilatéral et $\Gamma$ son cercle inscrit. Si $D$ et $E$ sont des points positionnés respectivement sur les côtés $AB$ et $AC$ de façon à ce que $DE$ soit tangent à $\Gamma$, montrez que \[ \frac{AD}{DB}+\frac{AE}{EC}=1 \]

  

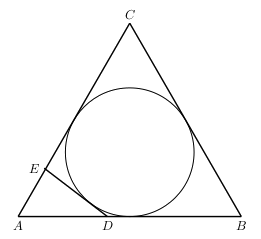
• Solution (publié le 4 octobre)

  Il s'agit du problème 4 de la 8^e Olympiade mathématique IberoAmerican. Celui-ci est apparu dans l'édition [1996:159-160] du Crux Mathematicorum. La solution suivante est celle de Sěfket Arslanagić et est apparue dans l'édition [1997:465-466].

  Soit $AB=AC=BC=a, BD=p$ et $CE=q$. Alors $AD=a-p$ et $AE=a-q$.

  

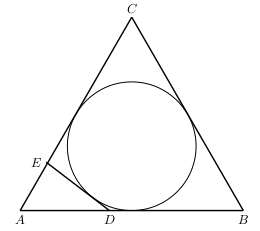
  Puisque le cercle $\Gamma$ est inscrit dans le quadrilatère $BCED$, on trouve que \[ ED+BC=BD+CE \,, \] ou autrement \[ED=p+q-a \,.\tag{1}\]

  Par la loi des cosinus dans le triangle $ADE$, on obtient \[ ED^2=AD^2+AE^2-2AD \cdot AE \cdot \cos(60^\circ) \,, \] et donc, avec l'équation $(1)$ on a \[ (p+q-a)^2=(a-p)^2+(a-q)^2-(a-p)(a-q) \,. \] En développant, on trouve \[ 3pq=ap+aq\,. \]

  Ainsi, \begin{align} \frac{AD}{DB}+\frac{AE}{EC} & = \frac{a-p}{p}+\frac{a-q}{q} \cr & = \frac{aq-pq+ap-qp}{pq} \cr & = \frac{ap+aq-2pq}{pq} \cr & = 1 \,. \end{align}

Semaine 3

• Problème (publié le 20 septembre)

  Soit $p$ le nombre de fonctions allant de $\{ 1, 2, 3, ..., m \}$, $m \in \mathbb{N}^{*}$ à $\{1, 2, ..., 35, 36\}$ et $q$ le nombre de fonctions allant de $\{ 1, 2, 3, ..., n \}$, $n \in \mathbb{N}^{*}$ à $\{1, 2, 3, 4, 5\}$. Déterminez la plus petite valeur possible de $|p-q|$.

• Solution (publié le 27 septembre)

  Il s'agit du problème 5 de la $40^{\text{ème}}$ Olympiade mathématique de Moldovie, form 11, qui est apparue dans le Crux Mathematicorum [2001:326-327]. On présente ici la solution légèrement modifiée de Pierre Bornsztein qui est apparue dans l'édition [1999:369-370].

  Soit $m,n \in \mathbb{N}^{*}$. On trouve que $p=36^m$ et $q=5^n$. Le problème est donc de trouver la valeur minimale de $|36^m-5^n|$ parmi toutes les valeurs de $m,n \in \mathbb{N}^{*}$.

  Les deux derniers chiffres de $36^m$ peuvent être $36, 96, 56, 16$ ou $76$. Les deux derniers chiffres de $5^n$ sont soit $05$ ou $25$.

  Ainsi, \[ 36^m-5^n \in \{ \pm 9, \pm 11, \pm 29, \pm 31, \pm 49 \} \pmod{100} \]

  On remarque aussi que puisque $9|36^m$ et $9 \nmid 5^n$ alors $9 \nmid 36^m-5m$. Donc $36^m-5^n \neq \pm 9$.

  Ceci nous montre que la plus petite valeur que peut prendre $|36^m-5^n|$ est $11$. Cette valeur est atteinte lorsque $m=n=2$.

  La plus petite valeur possible de $|p-q|$ est donc $11$.

Semaine 2

• Problème (publié le 13 septembre)

  Cette semaine on s'intéresse à une équation du cinquième degré.

  Trouvez toutes les solutions réelles à l'équation \[ 1+x+x^2+x^3=x^4+x^5 \,. \]

• Solution (publié le 20 septembre)

  C'est le problème 4 du $21^{\text{ème}}$ W.J. Blundon Mathematics Contest, Memorial University qui a été écrit en 2004 et donné dans la section Skoliad de l'édition [2005:354] du Crux Mathematicorum.

  Cette équation peut être réécrite sous la forme \[ (1+x)(1+x^2)=(1+x)x^4 \,. \]

  Sous cette forme, on remarque que $x=-1$ est une solution.

  Si $x \neq -1$ on peut diviser par $1+x$ pour obtenir \[ 1+x^2=x^4 \,, \] ou \[ x^4-x^2-1=0 \,. \]

  En faisant la substitution $y=x^2$, on trouve l'équation quadratique \[ y^2-y-1=0 \] dont les solutions sont \[ y_1= \frac{1+\sqrt{5}}{2} \mbox{ et } y_2= \frac{1-\sqrt{5}}{2} \,. \]

  Puisque $y_2 <0$, l'équation $x^2=y_2$ n'a pas de solution.

  À partir de $x^2=y_1$, on trouve deux nouvelles solutions réelles \[ x= \pm \sqrt{\frac{1+\sqrt{5}}{2}} \,. \]

  L'équation initiale a donc $3$ solutions réelles: \[ x=-1, x=\sqrt{\frac{1+\sqrt{5}}{2}} \mbox{ et } x=-\sqrt{\frac{1+\sqrt{5}}{2}} \,. \]

Semaine 1

• Problème (publié le 6 septembre)

  Voici deux problèmes plus simples pour cette première semaine. Essayez-les! La source du problème ainsi que la solution seront disponibles la semaine prochaine.}

  Problème A
  Dans l'image, $ABCD$ est un carré de côté 17 et les quatre triangles $ABF, DAE, BCG$ et $CDH$ sont congrus et rectangles. De plus, $\overline{FB}=8$. Déterminez l'aire de la région ombragée $EFGH$.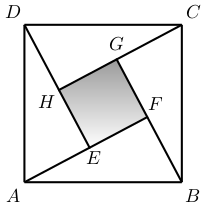

  

  Problème B
  Déterminez combien de paires entières $(x,y)$ sont solutions à l'équation \[ x^2y^3=6^{12} \,. \]

• Solution (publié le 13 septembre)

  Problème A

  Il s'agit du Problème 1 du BC Colleges High School Mathematics Contest 2005, ronde B de la finale junior, écrit en mai 2005 et donné dans la section Skoliad de l'édition [2005:265] du Crux Mathematicorum. La prochaine solution est la solution « officielle » qui est apparue dans l'édition [2006:137].

  Puisque $FB=8$ et $AB=17$, le théorème de Pythagore nous donne que $AF=15$. L'aire de chacun des quatre triangles congrus est donc $\frac{8 \times 15}{2}=60$. L'aire de la région ombragée $EFGH$ est donc $17^2-4\cdot 60=49$.

  Problème B

  Il s'agit du problème 3 du même concours que le précédent. On donne aussi la solution officielle apparue dans l'édition [2006:138].

  Premièrement, puisque $6^{12} >0$ et $x^2 \geq 0,$ il est nécessaire que $x^2 >0$ et que $y>0$.

  L'équation initiale est $x^2y^3=6^{12}=2^{12}3^{12}$. Puisque $x$ et $y$ divisent tous deux $2^{12}3^{12}$, on doit avoir $x= \pm 2^i3^j$ et $y= 2^k3^l$, où $i,j,k $ et $l$ sont des entiers positifs.

  On peut donc écrire $x^2=2^{2i}3^{2j}$ et $y^3=2^{3k}3^{3l}$. Ainsi, \[x^2y^3=2^{2i+3k}3^{2j+3l} \,.\]

  On doit obtenir $x^2y^3=2^{12}3^{12}$. Ainsi $2i+3k=12$ et $2j+3l=12$. Les solutions à ces deux équations sont \[ (i,k) \in \{ (0,4), (3,2), (6,0) \} \mbox{ et } (j,l) \in \{ (0,4), (3,2), (6,0) \} \,. \]

  Chacune des valeurs de $i$ peut être associée à chacune des valeurs de $j$. Une fois cette association faite, les valeurs de $k$ et $l$ sont déterminées. Le nombre de paires d'entiers positifs satisfaisant l'équation est donc $3 \times 3=9$. En admettant que $x$ puisse être négatif, on a $9 \times 2=18$ solutions.