31.

Find all continuous functions f: R ®R such that

View solution

32.

Let n ³ 3 be a natural number. Prove that

View solution

33.

Let n ³ 3 be a positive integer. Are there n positive integers a₁, a₂, ¼, a_n not all the same such that for each i with 3 £ i £ n we have

View solution

34.

Find all integers p for which there are rational numbers a and b such that the polynomial x⁵ - px - 1 has at least one root in common with the polynomial x² - ax - b.

35.

Let P be an arbitrary interior point of an equilateral triangle ABC. Prove that

View solution

36.

Let n be a positive integer and x > 0. Prove that

View solution

31.

First solution. Setting (x, y) = (t, 0) yields f(t + f(0)) = f(t) for all real t. Setting (x, y) = (0, t) yields f(f(t)) = f(0) + t for all real t. Hence f(f(f(t))) = f(t) for all real t, i.e., f(f(z)) = z for each z in the image of f. Let (x, y) = (f(t), -f(0)). Then

Taking (x, y) = (u, f(v)) yields

31.

Second solution. Taking (x, y) = (0, 0), we find that

31.

Third solution. Taking (x, y) = (0, 0) yields f(f(0)) = f(0), whence f(f(f(0))) = f(f(0)) = f(0). Taking (x, y) = (0, f(0)) yields f(f(f(0))) = 2f(0). Hence 2f(0) = f(0) so that f(0) = 0. Taking x = 0 yields f(f(y)) = y for each y. We can complete the solution as in the Second Solution.

32.

First solution. Let N = nⁿⁿⁿ - nⁿⁿ. Since 1989 = 3² ·13 ·17,

(i) x^u º 0 (mod 9) whenever u ³ 2 and x º 0 (mod 3).

(ii) x⁶ º 1 (mod 9) whenever x \not º 0 (mod 3).

(iii) x^u º 0 (mod 13) whenever x º 0 (mod 13).

(iv) x¹² º 1 (mod 13) whenever x \not º 0 (mod 13), by Fermat's Little Theorem.

(v) x^u º 0 (mod 17) whenever x º 0 (mod 17).

(vi) x¹⁶ º 1 (mod 17) whenever x \not º 0 (mod 17), by FLT.

(vii) x⁴ º 1 (mod 16) whenever x = 2y + 1 is odd. (For, (2y+1)⁴ = 16y³(y+2) + 8y(3y+1) + 1 º 1 (mod 16).)

Note that

Modulo 17. If n º 0 (mod 17), then nⁿⁿ º 0, and so N º 0 (mod 17).

If n is even, n ³ 4, then nⁿ º 0 (mod 16), so that

Suppose that n is odd. Then nⁿ º n (mod 4)

Modulo 13. If n º 0 (mod 13), then nⁿⁿ º 0 and N º 0 (mod 13).

Suppose that n is even. Then nⁿ º 0 (mod 4), so that nⁿⁿ - nⁿ º 0 (mod 4). Suppose that n is odd. Then n^{nn - n} - 1 º 0 (mod 16) and so nⁿⁿ - nⁿ º 0 (mod 4).

If n º 0 (mod 3), then nⁿ º 0 so nⁿ(n^{nn - n} - 1) º 0 (mod 3). If n º 1 (mod 3), then n^{nn - n} º 1 so nⁿ(n^nn-n - 1) º 0 (mod 3). If n º 2 (mod 3), then, as nⁿ - n is always even, n^nn-n º 1 so nⁿ(n^nn-n - 1) º 0 (mod 3). Hence, for all n, nⁿⁿ - nⁿ º 0 (mod 3).

It follows that nⁿⁿ - nⁿ º 0 (mod 12) for all values of n. Hence, when n is not a multiple of 13, n^{(nnn - n)} º 1 so N º 0 (mod 13).

Modulo 9. If n º 0 (mod 3), then nⁿⁿ º 0 (mod 9), so N º 0 (mod 9). Let n \not º 0 (mod 9). Since nⁿⁿ - nⁿ is divisible by 12, it is divisible by 6, and so n^{(nnn - nn)} º 1 and N º 0 (mod 9). Hence N º 0 (mod 9) for all n.

The required result follows.

33.

First solution. Letting b_i = (a_i, S_i), we find that

33.

Second solution. Let a_i = 1, a₂ = 2 and a_i = 3 ·2^i-3 for i ³ 3. Then

33.

Third solution. [K. Purbhoo] Choose a₁ at will, and let a_i = S_i-1 for i ³ 2. Then S_i = S_i-1 + a_i = 2a_i, a_i + S_i = 3a_i, (a_i, S_i) = a_i and [a_i, S_i] = 2a_i for i ³ 2.

33.

Fourth solution. [K. Yeats] Let a₁ = 1, a₂ = 3 and a_n = 2^n-1 for n ³ 3. Then S_n = 2ⁿ for n ³ 2 and, for each i with 3 £ i £ n, (a_i, S_i) = 2^i-1 and [a_i, S_i] = 2ⁱ.

34.

First solution. A common rational root must be 1 or -1, in which case the respective values of p are 0 and 2. These roots are shared with x² - 1 (a = 0, b = 1). Suppose that there is a common nonrational root r. Then r² = ar + b so that

34.

Second solution. The rational root case can be handled as in the first solution. By long division, we find that

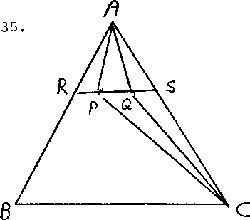
35.

First solution. The result is clear if P is on the bisector of the angle at A, since both sides of the inequality are 0.

Wolog, let P be closer to AB than AC, and let Q be the image of P under reflection in the bisector of the angle A. Then

Produce PQ to meet AB in R and AC in S. Consider the reflection  with axis RS. The circumcircle C of DARS is carried to a circle C¢ with chord RS. Since ÐRCS < 60^° = ÐRAS and the angle subtended at the major arc of C¢ by RS is 60^°, the point C must lie outside of C¢. The circumcircle D of DAPQ is carried by  to a circle D¢ with chord PQ. Since D is contained in C, D¢ must be contained in C¢, so C must lie outside of D¢. Hence ÐPQC must be less than the angle subtended at the major arc of D¢ by PQ, and this angle is equal to ÐPAQ. The result follows.

36.

First solution. By the Arithmetic-Geometric Means Inequality, we have that

36.

Second solution (by calculus). Let

36.

Third solution. Let u = nx - 1 so that x = (1 + u)/n. Then