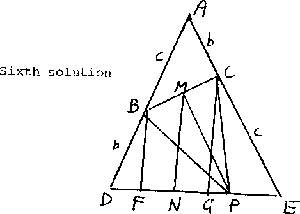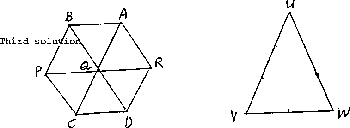Problem Set 3
- 13.
-
ABC is a triangle and D is a point on AB produced
beyond B such that BD = AC, and E is a point on AC produced
beyond C such that CE = AB. The right bisector of BC meets
DE at P. Prove that ÐBPC = ÐBAC.
-
-
(Note: This is Problem 2244 in CM+MM, May, 1997.)
View solution
- 14.
-
(a) Let a > b > c > d > 0 and a + d = b + c.
Show that ad < bc.
-
-
(b) Let a, b, p, q, r, s be positive integers for which
and qr - ps = 1. Prove that b ³ q + s.
View solution
- 15.
-
The Fibonacci sequence { Fn } is defined by
F1 = F2 = 1 and Fn+2 = Fn+1 + Fn for
n = 0, ±1, ±2, ±3, ¼. The real number t
is the positive solution of the quadratic equation
x2 = x + 1.
-
-
(a) Prove that, for each positive integer n,
F-n = (-1)n+1 Fn.
-
-
(b) Prove that, for each integer n, tn = Fn t+ Fn-1.
-
-
(c) Let Gn be any one of the functions Fn+1Fn,
Fn+1Fn-1 and Fn2. In each case, prove that
Gn+3 + Gn = 2(Gn+2 + Gn+1).
View solution
- 16.
-
(a) Show that, if
|
|
cosa
cosb
|
+ |
sina
sinb
|
= -1 , |
|
then
|
|
cos3 b
cosa
|
+ |
sin3 b
sina
|
= 1 . |
|
-
-
(b) Give an example of numbers a and b that
satisfy the condition in (a) and check that both equations hold.
View solution
- 17.
-
The sequence of functions { Pn } satisfies the
following relations:
|
P1 (x) = x , P2 (x) = x3 , |
|
|
Pn+1(x) = |
Pn3 (x) - Pn-1(x)
1 + Pn (x) Pn-1(x)
|
, n = 1, 2, 3, ¼. |
|
Prove that all functions Pn are polynomials.
View solution
- 18.
-
Each point in the plane is coloured with one of three
distinct colours. Prove that there are two points that are unit
distant apart with the same colour.
View solution
Solutions to Problem Set 3
13.
- 13.
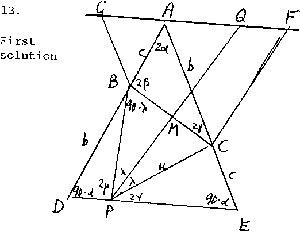
-
First solution. Let the lengths a, b, c, u and
the angles a, b, g, l, m, n
be as indicated in the diagram.
-
-
In the solution, we make use of the fact that if p/q = r/s,
then both fractions are equal to (p+r)/(q + s). Since
ÐDBP = 90° + l- 2b, it follows that
|
2m = 180° - (90° - a) - (90° +l- 2b) = a+ 2b- l . |
|
Similarly, 2n = a+ 2g- l.
Using the Law of Sines, we find that
|
| |
|
|
= |
b+c
sin2b+ sin2g
|
= |
b+c
2sin(b+ g)cos(b- g)
|
|
| |
|
| |
|
Hence
-
-
Since a = 2usinl and, by the Law of Sines,
|
|
u
sin(90° - a)
|
= |
b
sin2m
|
and |
u
sin(90° - a)
|
= |
c
sin2n
|
, |
|
we have that
|
| |
|
|
= |
u
cosa
|
= |
b
sin2m
|
= |
c
sin2n
|
= |
b+c
sin2m+ sin2n
|
|
| |
| = |
b+c
2sin(m+ n) cos(m- n)
|
= |
b+c
2coslcos(b- g)
|
= |
a
2coslsina
|
. |
|
| |
|
Hence tana = tanl and so a = l.
- 13.
-
Second solution. Let M be the midpoint of BC.
A rotation of 180° about M interchanges B and C and
takes E to G, D to F and P to Q. Then AB = CE = BG
and AC = BD = CF. Join GA and FA. Let 2a = ÐBAC.
Since AE || BG and AB is a transversal, ÐGBA = ÐBAC = 2a. Since AB = BG, ÐBGA = 90°- a. But ÐBGF = ÐCED = 90° - a.
Thus, G, A, F are collinear.
-
-
Since GF and DE are equidistant from M, we can use
Cartesian coordinates with the origin at M, the line y = 1 as
GF and the line y = -1 as DE. Let A ~ (a, 1),
B ~ (-u, -mu), C ~ (u, mu). Then P ~ (m, -1),
Q ~ (-m, 1),
|
D ~ (a - |
2(a+u)
1 + mu
|
, -1), E ~ (a + |
2(a+u)
1 + mu
|
, -1) . |
|
Since |AC | = |BD |, we find that
u - a = -u - a + [(2(a+u))/(1 + mu)], or a = mu2.
(We can check this by equating the slopes of AC and AE.)
-
-
The slope of AE is -1/u and of AD is 1/u, so that
|
tanÐBAC = |
-(2/u)
1 - (1/u2)
|
= - |
2u
u2 - 1
|
. |
|
The slope of CQ is (mu - 1)/(m+u) and of BQ is
(1 + mu)/(u-m), so that
|
| |
|
|
= |
(mu - 1)(u - m) - (mu + 1)(u + m)
(u - m)(u + m) + (mu - 1)(mu + 1)
|
|
| |
| = |
-2(m2 u + u)
u2 - m2 + m2 u2 - 1
|
= |
-2(m2 + 1)u
(1 + m2)(u2 - 1)
|
= |
-2u
u2 - 1
|
. |
|
| |
|
The result follows.
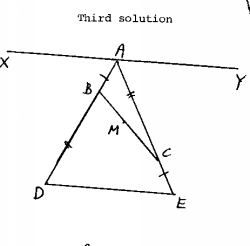
- 13.
-
Third solution. [M. Boase] Let XAY be drawn
parallel to DE.
-
-
Since M is the midpoint of BC, the distance from M
to DE is the average of the distances from B and C to DE.
Similarly, the distance from M to XY is the average of the
distances from B and C to XY. The distance of B (resp. C)
to DE equals the distance of C (resp. B) to XY. Hence,
M is equidistant from DE and XY. If PM produced meets
XY in Q, then PM = MQ and so ÐBQC = ÐBPC.
-
-
Select R on MQ (possibly produced) so that ÐBAC = ÐBRC. Since DADE ||| DRBC,
ÐRBC = ÐRCB = ÐADE. Since BARC is
a concyclic quadrilateral, ÐBAR = 180° - ÐRCB = 180° - ÐADE = 180°- ÐXAD = ÐBAQ from which it follows that
R = Q and so ÐBPC = ÐBQC = ÐBRC = ÐBAC.
- 13.
-
Fourth solution. [Jimmy Chui] Set coordinates:
A ~ (0, (m+n)b), B ~ (-ma, nb), C ~ (na, mb)
D ~ (-(m+n)a, 0) and E ~ ((m+n)a, 0) where
m = |AB |, n = |AC | and a2 + b2 = 1. Then
the line BC has the equation
|
|
m-n
a
|
x - |
m+n
b
|
y + m2 + n2 = 0 |
|
and the right bisector of BC has equation
|
|
m+n
b
|
x + |
m-n
a
|
y + |
(a2 - b2)(m2 - n2)
2ab
|
= 0 . |
|
Thus
|
P ~ |
æ
ç
è
|
|
(b2 - a2)(m - n)
2a
|
, 0 |
ö
÷
ø
|
. |
|
Now
|
|BC |2 = m2 + n2 + 2mn(a2 - b2) |
|
and
|
|BP |2 = |
m2 + n2 + 2mn(a2 - b2)
4a2
|
|
|
so that
|BC |/ |BP | = 2a. Also
|DE |/ |AD | = 2(m+n)a/(m+n) = 2a
so that DBPC is similar to DADE and the result
follows.
- 13.
-
Fifth solution. Determine points L and N on
DE such that BL || AE and LN = NE. Now
so that CL || AD and CL:AD = CE:AE. Since AD = DE, CL = CE
and so CN ^LE. Consider the trapezoid CBLE. The line
MN joins the midpoints of the nonparallel opposite sides and so
MN || BL. MPNC is a quadrilateral with right angles at
M and N, and so is concyclic. Hence
|
ÐBPC = 2ÐMPC = 2ÐMNC = 2ÐNCE = ÐLCE = ÐBAC . |
|
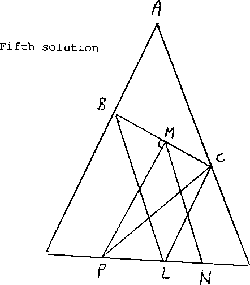
- 13.
-
Sixth solution. [C. So] Let F, N, G be the feet
of the perpendiculars dropped from B, M, C respectively to DE.
Note that FN = NG, so that MF = MG.
Let ÐADE = ÐAED = q, |AB | = c,
|AC | = b and h be the altitude of DADE. Then
|
|MN | = |
1
2
|
[ |BF |+ |CG |] = |
1
2
|
(b + c)sinq = |
h
2
|
|
|
and
|
|DF | = b cosq , |GE | = c cosq , |DE | = 2(b + c)cosq . |
|
Hence |FG | = |DE |- |DF |- |GE | = 1/2 |DE |. Since DADE and DMFG are
isosceles triangles with heights and beses in proportion, they are
similar so that ÐMFG = ÐADE = q. Since
ÐBFP = ÐBMG = 90°, the quadrilateral BFPM is
concyclic and so ÐCBP = ÐMFP = q (we are supposing
that the configuration is labelled so P lies between F and E).
Hence DADE is similar to DPCB and so ÐBPC = ÐBAC.
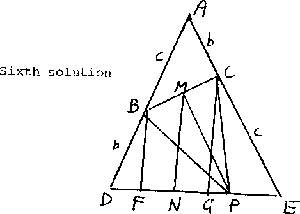
- 13.
-
Seventh solution. [A. Chan] Let ÐADE = ÐAED = q, so ÐBAC = 180° - 2q. Suppose that
ÐACB = f, ÐCPE = s and ÐBCP = r.
By the Law of Sines for triangles ABC and PCE, we find that
|
|
2 |PC |cosr
sin2q
|
= |
|AB |
sinf
|
|
|
whence
|
|
sins
sinq
|
= |
|CE |
|PC|
|
= |
|AB |
|PC |
|
= |
2 cosrsinf
sin2q
|
|
|
and
Therefore
|
sin(q+ s) + sin(s- q) = sin(f+ r) + sin(f- r). |
|
Since q+ s = f+ r, sin(s- q) = sin(f- r). Either (s- q) + (f- r) = ±180° or s- q = f- r. In the
first case, since q+ s = f+ r, |s- r| = 90°, which is false.
-
-
Hence s- q = f- r, so, with q+ s = f+ r, we have that
|
2 q = q+ (r+ s- f) = q+(r+ r- s) = 2r |
|
and the result follows.
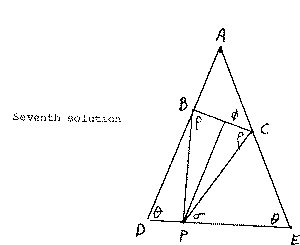
14.
- 14.
-
(a) First solution. Since c = a + d - b, we have
that
|
bc - ad = b(a + d - b) - ad = (a - b)b - (a - b)d = (a - b)(b - d) > 0 . |
|
-
-
(a) Second solution. Let a + d = b + c = u. Then
|
bc - ad = b(u - b) - (u - d)d = u(b - d) - (b2 - d2) = (b - d)(u - b - d) . |
|
Now u = b + c > b + d, so that u - b - d > 0 as well as b - d > 0.
Hence bc - ad > 0 as desired.
-
-
(a) Third solution. Let x = a - b > 0. Since
a - b = c - d, we have that a = b + x and d = c - x. Hence
|
bc - ad = bc - (b + x)(c - x) = bx - cx + x2 = x2 + x(b - c) > 0 . |
|
-
-
(a) Fourth solution. Since Öa > Öb > Öc > Öd, Öa - Öd > Öb - Öc.
Squaring and using a + d = b + c yields 2Ö[bc] > 2Ö[ad],
whence the result.
- 14.
-
(b) First solution. Since all variables represent
integers,
|
aq - bp > 0, br - as > 0 Þ aq - bp ³ 1,br - as ³ 1 . |
|
Therefore
|
b = b(qr - ps) = q(br - as) + s(aq - bp) ³ q + s . |
|
15.
- 15.
-
(a) First solution.
Since F0 = F2 - F1 = 0,
the result holds for n = 0. Since F-1 = F1 - F0 = 1, the
result holds for n = 1. Suppose that we have established the
result for n = 0, 1, 2, ¼r. Then
|
F-(r+1) = F-r-1 = F-r+1 - F-r = (-1)r Fr-1- (-1)r+1 Fr = (-1)r+2(Fr-1 + Fr) = (-1)r+2Fr+1 . |
|
The result follows by induction.
- 15.
-
(b) First solution. The result holds for n = 0,
n = 1 and n = 2. Suppose that it holds for n = 0, 1, 2, ¼,r. Then
|
tr+1 = tr + tr-1 = (Fr + Fr-1)t+ (Fr-1 + Fr-2) = Fr+1t+ Fr t . |
|
This establishes the result for positive values of n.
Now t-1 = t- 1 = F-1t+ F-2, so the result
holds for n = -1. Suppose that we have established the result
for n = 0, -1, -2, ¼, -r. Then
|
t-(r+1) = t-(r-1) - t-r = (F-(r-1) - F-r)t+ (F-r - F-(r+1)) = F-(r+1)t+ F-(r+2) . |
|
- 15.
-
(b) Second solution. The result holds for
n = 1. Suppose that it holds for n = r ³ 0. Then
|
tr+1 = tr ·t = (Fr t+ Fr-1) t = Fr t2 + Fr-1t |
|
|
= (Fr + Fr-1)t+ Fr = Fr+1 t+ Fr . |
|
Now consider nonpositive values of n. We have that
t0 = 1, t-1 = t- 1, t-2 = 1 - t-1 = 2 - t. Suppose that we have shown for r ³ 0 that
t-r = F-r t+ F-r-1. Then
|
t-(r+1) = t-1 t-r = F-r + F-r-1(t- 1) = F-r-1 t+ (F-r - F-r-1) |
|
|
= F-r-1t+ F-r-2 = F-(r+1)t+ F-(r+1)-1 . |
|
By induction, it follows that the result holds for both positive and
negative values of n.
- 15.
-
(c) First solution. Let Gn = Fn Fn+1.
Then
|
| |
|
| |
|
= (Fn+3 + Fn+2)(Fn+2 + Fn+1) +(Fn+3 - Fn+2)(Fn+2 - Fn+1) |
| |
| = 2(Fn+3 Fn+2 + Fn+2 Fn+1) = 2(Gn+2 + Gn+1) . |
|
| |
|
-
-
Let Gn = Fn+1Fn-1. Then
|
| |
|
| |
|
= (Fn+3 + Fn+2)(Fn+1 + Fn) +(Fn+3 - Fn+2)(Fn+1 - Fn) |
| |
| = 2(Fn+3 Fn+1 + Fn+2 Fn) = 2(Gn+2 + Gn+1) . |
|
| |
|
-
-
Let Gn = Fn2. Then
|
| |
|
|
= Fn+32 + Fn2 = (Fn+2 + Fn+1)2 + (Fn+2 - Fn+1)2 |
| |
| = Fn+22 + 2Fn+2Fn+1 + Fn+12+ Fn+22 - 2Fn+2Fn+1 + Fn+12 = 2(Gn+2 + Gn+1) . |
|
| |
|
-
-
Comments. Since Fn2 = Fn Fn-1 + Fn Fn-2,
the third result of (c) can be obtained from the first two.
J. Chui observed that, more generally, we can take
Gn = Fn+uFn+v where u and v are integers. Then
|
| |
|
| |
|
= (Fn+3+uFn+3+v + Fn+uFn+v) - 2(Fn+2+uFn+2+v + Fn+1+uFn+1+v) |
| |
|
= (2Fn+1+u + Fn+u)(2Fn+1+v + Fn+v) + Fn+uFn+v |
| |
|
- 2(Fn+1+u + Fn+u)(Fn+1+v + Fn+v) - 2Fn+1+uFn+1+v |
| |
|
| |
|
so that Gn+3 + Gn = 2(Gn+2 + Gn+1).
16.
- 16.
-
(a) First solution.
Let
|
l = |
cosb
cosa
|
and m = |
sinb
sina
|
. |
|
Since l-1 + m-1 = -1, we have that
l+ m = -lm.
Now
|
1 = cos2 b+ sin2 b = l2 cos2 a+ m2 sin2 a = l2 + (m2 - l2)sin2a = l2 - (m- l)lmsin2 a . |
|
Hence
|
| |
|
| |
|
= l(l2 cos2 a+ m2 sin2 a) + (m- l)m2 sin2 a |
| |
| |
| |
| |
|
| |
|
- 16.
-
(a) Second solution. [M. Boase]
|
|
cosa
cosb
|
+ |
sina
sinb
|
= -1 Þ |
|
|
sin(a+ b) + sinbcosb = 0 . (*) |
|
Therefore
|
| |
|
|
= |
cosb(1 - sin2 b)
cosa
|
+ |
sinb(1 - cos2 b)
sina
|
|
| |
|
= |
cosb
cosa
|
+ |
sinb
sina
|
- sinbcosb |
æ
ç
è
|
|
sinb
cosa
|
+ |
cosb
sina
|
|
ö
÷
ø
|
|
| |
|
= |
sin(a+ b)
cosasina
|
- |
cosbsinb(cos(a- b))
cosasina
|
|
| |
|
= |
-2 sinbcosb+ 2 sin(a+ b) cos(a- b)
2 sinacosa
|
using (*) |
| |
| = |
-2 sinbcosb+ [sin2a+ sin2b]
sin2a
|
= 1 |
|
| |
|
since 2 sinbcosb = sin2b.
- 16.
-
(a) Third solution. [A. Birka] Let
cosa = x and cosb = y. Then
Since
then
|
(x2 + 2xy + y2)(1 - y2) = y2(1 - x2) , |
|
whence
Thus,
|
| |
|
| |
|
= |
y3
x
|
- |
(1 - y2)y
x + y
|
= |
y4 + 2xy3 - xy
x(x+y)
|
|
| |
|
| |
|
- 16.
-
(a) Fourth solution. [J. Chui] Note that the
given equation implies that sin2b = -2sin(a+ b)
and that the numerator of
|
|
cosa
cosb
|
+ |
sina
sinb
|
+ |
cos3 b
cosa
|
+ |
sin3 b
sina
|
|
|
is one quarter of
|
| |
|
|
+ sin2 acosacosb+cos4 bsinasinb+ sin4 bcosacosb] |
| |
|
= 4[cos2 asinasinb+ sin2 acosacosb+ (cos2 b- cos2 bsin2 b)sinasinb |
| |
|
+ (sin2 b- sin2 bcos2 b)cosacosb] |
| |
|
= (4cos2 a+ 4cos2 b- sin2 2b)sinasinb+ (4sin2 a+ 4sin2 b- sin2 2b)cosacosb |
| |
|
= 2sin2acosasinb+ 2sin2bcosbsina+ 2sin2asinacosb+2sin2bcosasinb |
| |
|
- sin2 2b(cosacosb+ sinasinb) |
| |
|
= 2(sin2a+ sin2b) sin(a+ b)- sin2 2bcos(a- b) |
| |
| = 2sin(a+ b) [sin2a+ sin2b-2sin(a+ b)cos(a- b)] = 0 , |
|
| |
|
since
|
sin2a+ sin2b = sin( |
a+ b
|
+ |
a- b
|
)+ sin( |
a+ b
|
- |
a- b
|
) . |
|
- 16.
-
(a) Fifth solution. [A. Tang] From the given
equation, we have that
|
|
cosb
cosa
|
= |
-sinb
sina+ sinb
|
, |
|
and
|
|
sinb
sina
|
= |
-cosb
cosa+ cosb
|
. |
|
Hence
|
| |
|
|
= cos2b |
é
ê
ë
|
|
-sinb
sina+ sinb
|
|
ù
ú
û
|
+ sin2 b |
é
ê
ë
|
|
-cosb
cosa+ cosb
|
|
ù
ú
û
|
|
| |
|
= - |
sinbcosb[cosacosb+sinasinb+ 1]
|
4 sin |
1
2
|
(a+ b) cos |
1
2
|
(a-b) cos |
1
2
|
(a+ b) cos |
1
2
|
(a- b) |
|
|
| |
| = |
sin(a+ b) [cos(a- b) + 1]
|
[2 sin |
1
2
|
(a+ b) cos |
1
2
|
(a+ b)][2 cos2 |
1
2
|
(a- b)] |
|
= 1 . |
|
| |
|
- 16.
-
(a) Sixth solution. [D. Arthur] The given equations
yield 2 sin(a+ b) = -sin2b,
cosasinb = -cosb(sina+ sinb)
and sinacosb = -sinb(cosa+ cosb).
Hence
|
| |
|
|
= |
cos2 b(cosbsina) + sin2 b(sinbcosa)
cosasina
|
|
| |
|
= |
- cos2 bsinb(cosa+ cosb) -sin2 bcosb(sina+ sinb)
cosasina
|
|
| |
|
= |
- cosbsinb(cosacosb+ cos2 b+ sinasinb+ sin2 b)
cosasina
|
|
| |
|
= |
- sin2b(1 + cos(a- b))
sin2a
|
|
| |
|
= |
- sin2b+ 2sin(a+ b)cos(a- b)
sin2a
|
|
| |
| = |
- sin2b+ sin2a+ sin2b
sin2a
|
= 1 . |
|
| |
|
- 16.
-
(b) First solution. The given equation is equivalent to
2 sin(a+ b) + sin2b = 0. Try b = -45°
so that sin(a- 45°) = 1/2. We take
a = 75°. Now
|
sin75° = sin(45° + 30°) = |
1
Ö2
|
|
æ
ç
è
|
|
Ö3 + 1
2
|
|
ö
÷
ø
|
|
|
and
|
cos75° = cos(45° + 30°) = |
1
Ö2
|
|
æ
ç
è
|
|
Ö3 - 1
2
|
|
ö
÷
ø
|
. |
|
It is straightforward to check that both equations hold.
17.
- 17.
-
First solution. Taking x = 1, 2, 3, ¼ yields
the respective sequences
|
{ 1, 1, 0, -1, -1, 0, ¼} , { 2, 8, 30, 112, 418, 1560, ¼} , { 3, 27, 240, 2133, ¼} . |
|
In each case, we find that
|
Pn+1(x) = x2 Pn (x) - Pn-1(x) (1) |
|
for n = 2, 3, ¼.
If we can establish (1) in general, it will follow that all the
functions Pn are polynomials.
-
-
From the definition of Pn, we find that
|
Pn+1 + Pn-1 = Pn (Pn2 - Pn+1Pn-1) . |
|
Therefore, it suffices to establish that Pn2 - Pn+1Pn-1 = x2 for each n. Now, for n ³ 2,
|
| |
|
|
-[Pn2 - Pn+1Pn-1] = Pn+1(Pn+1 + Pn-1) - Pn (Pn+2 + Pn) |
| |
|
= Pn+1Pn(Pn2 - Pn+1Pn-1) - Pn Pn+1(Pn+12 - Pn+2Pn) |
| |
| = -Pn+1Pn [(Pn+12 - Pn+2Pn) -(Pn2 - Pn+1Pn-1)] , |
|
| |
|
so that either Pn+1(x)Pn(x) + 1 º 0 or
Pn+12 - Pn+2Pn = Pn2 - Pn+1Pn-1. The first
identity is precluded by the case x = 1, where it is false.
Hence
|
Pn+12 - Pn+2Pn = Pn2 - Pn+1Pn-1 |
|
for n = 2, 3, ¼. Since P2 2 (x) - P3(x)P1(x) = x2,
the result follows.
- 17.
-
Second solution. [By inspection, we make the
conjecture that Pn (x) = x2 Pn-1(x) - Pn-2. Rather than
prove this directly from the rather awkward condition on Pn,
we go through the back door.] Define the sequence { Qn }
for n = 0, 1, 2, ¼ by
|
Q0(x) = 0 , Q1(x) = x , Qn+1 = x2 Qn (x) - Qn-1(x) |
|
for n ³ 1. It is clear that Qn (x) is a polynomial of
degree 2n - 1 for n = 1, 2, ¼. We show that Pn(x) = Qn (x) for each n.
-
-
Lemma: Qn2 (x) - Qn+1Qn-1 = x2 for n ³ 1.
-
-
Proof: This result holds for n = 1. Assume that it
holds for n = k-1 ³ 1. Then
|
| |
|
|
= Qk2 (x) - (x2 Qk (x) - Qk-1(x))Qk-1(x) |
| |
|
= Qk (x) (Qk(x) - x2 Qk-1(x)) + Qk-12 (x) |
| |
| = -Qk (x) Qk-2 (x) + Qk-12 (x) = x2 . QED |
|
| |
|
-
-
From the lemma, we find that
|
| |
|
|
+ Qn-1(x) + Qn+1(x) Qn(x) Qn-1(x) |
| |
| = x2 Qn (x) + Qn+1(x) Qn (x) Qn-1(x) = Qn (x)(x2 + Qn+1 (x) Qn-1(x)) = Qn3(x) |
|
| |
|
|
Þ Qn+1(x) = |
Qn3(x) - Qn-1(x)
1 + Qn (x) Qn-1(x)
|
(n = 1, 2, ¼) . |
|
We know that Q1 (x) = P1 (x) and Q2 (x) = P2 (x). Suppose that
Qn (x) = Pn (x) for n = 1, 2, ¼, k. Then
|
Qk+1 (x) = |
Qk3 (x) - Qk-1(x)
1 + Qk (x) Qk-1(x)
|
= |
Pk3 (x) - Pk-1(x)
1 + Pk (x) Pk-1(x)
|
= Pk+1(x) |
|
from the definition of Pk+1. The result follows.
-
-
Comment: It can also be established that
Pn+12 + Pn2 = (1 + Pn Pn+1)x2 for each n ³ 0.
- 17.
-
Third solution. [I. Panayotov] First note that
the sequence { Pn (x) } is defined for all values of
x, i.e., the denominator 1 + Pn-1(x)Pn(x) never
vanishes for n and x. Suppose otherwise, and let n be the
least number for which there exists u for which 1 + Pn-1(u)Pn (u) = 0. Then n ³ 3 and
|
-1 = Pn-1(u) Pn(u) = |
Pn-1(u)4 - Pn-1(u)Pn-2(u)
1 + Pn-1(u)Pn-2(u)
|
|
|
which implies that
Pn-1(u)4 = -1, a contradiction.
-
-
We now prove by induction that Pn+1 = x2 Pn - Pn-1.
Suppose that Pk = x2 Pk-1 - Pk-2 for 3 £ k £ n,
so that in particular we know that Pk is a polynomial for
1 £ k £ n. Substituting for Pk yields
|
Pk-13(x) = Pk-1(x)[x2 + x2 Pk-1(x)Pk-2(x)- Pk-22(x)] |
|
for all x. If Pk-1(x) ¹ 0, then
|
Pk-12 (x) = x2 + x2Pk-1Pk-2(x) - Pk-22(x) . |
|
Both sides of this equation are polynomials and so continuous functions
of x. Since the roots of Pk-1 constitute a finite discreet
set, this equation holds when x is one of the roots as well.
Now
|
| |
|
|
= |
Pn3 - Pn-1
1 + Pn Pn-1
|
= |
Pn (x2 Pn-1 - Pn-2)2 - Pn-1
1 + Pn Pn-1
|
|
| |
|
= |
Pn (x4 Pn-12 - x2 Pn-1Pn-2 + x2 - Pn-12) - Pn-1
1 + Pn Pn-1
|
|
| |
|
= |
Pn (x2 Pn Pn-1 + x2 - Pn-12) - Pn-1
1 + PnPn-1
|
since x2 Pn-1 - Pn-2 = Pn |
| |
| = |
(x2 Pn - Pn-1)(1 + Pn Pn-1)
1 + Pn Pn-1
|
= x2 Pn - Pn-1 . |
|
| |
|
The result follows.
18.
- 18.
-
First solution. Suppose that the points in the plane
are coloured with three colours. Select any point P.
-
-
Consider the diagrammed configuration, in which all segments
have length 1. If P, Q, R are all coloured differently, then
either the result holds or
S must have the same colour as P. If P, U, V are all coloured
differently, then either the result holds or
W must have the same colour as P. Hence, either
one of the triangles PQR and PUV has two vertices the same colour,
or else S and W must be coloured the same.
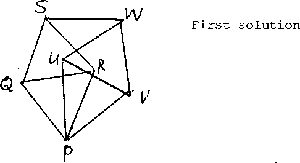
- 18.
-
Second solution. Suppose, if possible, the planar points
can be coloured without two points unit distance apart being coloured the
same. Then if A and B are distant Ö3 apart, then there
are distinct points C and D such that ACD and BCD are
equilateral triangles (ABCD is a rhombus). Since A and B must
be coloured differently from the two colours of C and D,
A and B must have the same colour. Hence, if O is any point
in the plane, every point on the circle of radius Ö3
consists of points coloured the same as O. But there are
two points on this circle unit distant apart, and we get a contradiction
of our initial assumption.
- 18.
-
Third solution. Suppose we can colour the points of
the plane with three colours, red, blue and yellow so that
the result fails. We show that
three collinear points at unit distance are coloured with three
different colours. Let P, Q, R be three such points, and embed
P, Q, R in the hexagon ABPCDR as indicated with all indicated
segments of unit length.
-
-
If, say, Q is red, B and A must be coloured differently,
as are A and R, R and D, D and C, C and P, P and
B. Thus, B, R, C, are one colour, say, blue, and A, D,
P the other, say yellow. The preliminary result follows.
-
-
Now consider any isosceles triangle UVW with |UV | = |UW | = 3 and |VW | = 2. It
follows from the preliminary result that U and V must have the
same colour, as do U and W. But V and W cannot have the
same colour and we reach a contradiction.
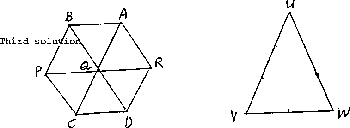
- 18.
-
Fourth solution. [D. Arthur] Suppose that the
result is false. Let A, B be two points with |AB | = 3. Within the segment AB select PQ with |AP | = |PQ | = |QB | = 1, and suppose that R and
S are points on the same side of AB with DRAP and
DSPQ equilateral. Then |RS | = 1. Suppose if
possible that A and Q have the same colour. Then P must
have a second colour and R and S the third, leading to a
contradiction. Hence A must be coloured differently from both
P and Q. Similarly B must be coloured differently from
both P and Q. Since P and Q are coloured differently,
A and B must have the same colour.
-
-
Now consider a trapezoid ABCD with |CB | = |AB| = |AD | = 3 and |CD | = 1. By the
foregoing observation, C, A, B, D must have the same
colour. But this yields a contradiction. The result follows.