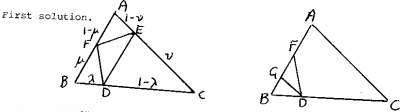MOCP 1997-1998 Problem Set 2

Problem Set 2

7.: For each of the following expressions independently, determine as many integer values of x as you can that it is a perfect square. Indicate whether your list is complete or not.

: (a) 1 + x;

: (b) 1 + x + x²;

: (c) 1 + x + x² + x³;

: (d) 1 + x + x² + x³ + x⁴;

: (e) 1 + x + x² + x³ + x⁴ + x⁵.

View solution

8.: Let ABC be an arbitrary triangle with the points D, E, F on the sides BC, CA, AB respectively, so that

£ 1

and

Prove that [DEF] £ ¹/₄[ABC], with equality if and only if two at least of the three points D, E, F are midpoints of the corresponding sides.

(Note: [XYZ] denotes the area of triangle XYZ. This is Problem 2240 in CM+M², May, 1997.)
View solution

9.: ABCD is a square with incircle G. Let l be a tangent to G, and A¢, B¢, C¢, D¢ be points on l such that AA¢, BB¢, CC¢, DD¢ are all perpendicular to l. Prove that AA¢·CC¢ = BB¢·DD¢.

: (Note: XY here and in the previous problem denotes the length of the segment XY; the dot is ordinary multiplication. This is Problem 2237 in CM+MM, April, 1997.)

View solution

10.: (a) Three ants crawl along the sides of a fixed triangle in such a way that the centroid (intersection of the medians) of the triangle they form at any moment remains constant. Show that this centroid coincides with the centroid of the fixed triangle if one of the ants travels along the entire perimeter of the triangle.

: (b) Is it indeed always possible for a given fixed triangle with one ant at any point on the perimeter of the triangle to place the remaining two ants somewhere on the perimeter so that the centroid of their triangle coincides with the centroid of the fixed triangle?

View solution

11.: The faces of a tetrahedron are formed by congruent triangles. If a is the angle between a pair of opposite edges of the tetrahedron, show that

cosa =

sin(B-C)

sin(B+C)

where B and C are the angles adjacent to one of these edges in a face of the tetrahedron.
View solution

12.: (a) Give an example of a pair a, b of positive integers, not both prime, for which 2a - 1, 2b - 1 and a + b are all primes. Determine all possibilities for which a and b are themselves prime.

: (b) Suppose a and b are positive integers such that 2a - 1, 2b - 1 and a + b are all primes. Prove that neither a^b + b^a nor a^a + b^b are multiples of a + b.

View solution

Solutions to Problem Set 2

7.: (a) 1 + x is a square when x = u² - 1 for some integer u (or when x is the product of two integers u-1 and u+1 that differ by 2).

7.: (b) First solution. Suppose that x² + x + 1 = u². Then (2x + 1)² + 3 = 4x² + 4x + 4 = 4u² = (2u)², whence

3 = (2u)² - (2x + 1)² = (2u + 2x + 1)(2u - 2x - 1) .

The factors on the right must be ±3 and ±1 in some order, and this leads to the possibilities (x, u) = (-1, ±1),(0, ±1).

: (b) Second solution. If x > 0, then x² < x² + x + 1 < (x + 1)², so that x² + x + 1 cannot be square. If x < -1, then x² > x² + x + 1 > (x + 1)² and x² + x + 1 cannot be square. This leaves only the possibilities x = 0, -1.

: (b) Third solution. For given u, consider the quadratic equation

x² + x + 1 = u² .

Its discriminant is 1 - 4(1 - u²) = 4u² - 3. It will have integer solutions only if 4u² - 3 = v² for some integer v, i.e., (v + 2u)(v - 2u) = -3. The only possibilities are (u, v) = (±1, ±1), (±1, -±1).

: (b) Fourth solution. [J. Chui] If f(x) = 1 +x + x², then f(x) = f(-(x+1)), so we need deal only with nonnegative values of x. We have that f(0) = f(-1) = 1 is square. Let x ³ 1 and suppose that 1 + x + x² = u² for some integer u. Then (1 + x)² - u² = x > 0 so that 1 + x > u. This implies that x ³ u, whence x² ³ u² = x² + x + 1, a contradiction. Thus the only possibilities are x = 0, -1.

: (b) Fifth solution. [A. Birka] Suppose that x² + x + 1 = u² with u ³ 0. This is equivalent to x = (1 + x)² - u² = (1 + x + u)(1 + x - u), so that 1 + x + u and 1 + x - u both divide x. If x ³ 1, then 1 + x + u exceeds x and so cannot divide x. If x £ 0, then (-x) + u - 1 divides x, which is impossible unless u = 1 or u = 0. Only u = 1 is viable, and this leads to x = 0, -1.

7.: (c) First solution. 1 + x + x² + x³ = (1 + x²)(1 + x). Let d be a common prime divisor of 1 + x and 1 + x². Then d must also divide x(x - 1) = (1 + x²) - (1 + x). Since gcd(x, x + 1) = 1, d must divide x - 1 and so divide 2 = (x + 1) - (x - 1). Hence, the only common prime divisor of 1 + x² and 1 + x is 2.

: Suppose 1 + x + x² + x³ = (1 + x²)(1 + x) is square. Then there are only two possibilities:

(i) 1 + x² = u² and 1 + x = v² for integers u and v ;

(ii) 1 + x² = 2r² and 1 + x = 2s² for integers r and s .

: Ad (i): 1 = u² - x² = (u - x)(u + x) Û(x, u) = (0, ±1).

: Ad (ii): We have x² - 2r² = -1 which has solutions

(x, r) = (-1, 1), (1, 1), (7, 5), (41, 29), ¼ .

The complete set of solutions of x² - 2r² = ±1 in positive integers is given by { (x_n, r_n) : n = 1, 2, ¼}, where x_n + r_n Ö2 = (1 + Ö2)ⁿ, with odd values of n yielding solutions of x² - 2r² = -1. We need to select values of x for which x + 1 = 2s² for some s. x = -1, 1, 7 work, yielding

1 - 1 + (-1)² + (-1)³ = 0

1 + 1 + 1² + 1³ = 2²

1 + 7 + 7² + 7³ = 8 ×50 = 20² .

There may be other solutions.

7.: (d) First solution. Let f(x) = x⁴ + x³ + x² + x +1 = (x⁵ - 1)/(x - 1), with the quotient form for x ¹ 1. We have that f(0) = f(-1) = 1² and f(3) = (243 - 1)/2 = 11². Also f(1) = 5 and f(2) = 31. Suppose that x ³ 4. Then x(x - 2) > 3, so that x² > 2x + 3. Hence

(2x² + x + 1)²

= 4x⁴ + 4x³ + 5x² + 2x + 1

> 4x⁴ + 4x³ + 4x² + 4x + 4 = 4f(x)

and

4f(x)

= (4x⁴ + 4x³ + x²) + (3x² + 4x + 4)

= (2x² + x)² + (3x² + 4x + 4) > (2x² + x)² .

Thus, 4f(x) lies between the consecutive squares (2x² + x)² and (2x² + x + 1)² and so cannot be square. Hence f(x) cannot be square.

: Similarly, if x £ -2, then x(x - 2) > 3 and 3x² + 4x + 4 > 0, and we again find that 4f(x) lies between the consecutive squares (2x² + x)² and (2x² + x + 1)². Hence f(x) is square if and only if x = -1, 0, 3.

: (d) Second solution. [M. Boase] For x > 3,

(x² +

)² < x⁴ + x³ + x² + x + 1 < (x² +

x+1

)²

so that, lying between two half integers, x⁴ + x³ + x² + x + 1 is not square. Suppose x = -y is less than -1. Since y - 1 < ³/₄y² and y² + 2y - 3 = (y + 3)(y - 1) > 0,

(y² -

)² < 1 - y + y² - y³ + y⁴ < (y² -

y-1

)²

so again the middle term is not square. The cases x = -1, 0, 1, 2, 3 can be checked directly.

7.: (e) First solution. Let

g(x)

= x⁵ + x⁴ + x³ + x² + x + 1 = (x + 1)(x⁴ + x² + 1)

= (x + 1)[(x² + 1)² - x²] = (x + 1)(x² + x + 1)(x² - x + 1) .

Observe that g(x) < 0 for x £ 2, so g(x) cannot be square in this case. Let us analyze common divisors of the three factors of g(x).

: Suppose that p is a prime divisor of x + 1. Then

x² + x + 1 = x(x + 1) + 1 º 1 mod p

and

x² - x + 1 = x(x + 1) - 2(x + 1) + 3 º 3 mod p .

Hence gcd(x + 1, x² + x + 1) = 1 and gcd(x + 1, x² - x + 1) is either 1 or 3.

: Suppose q is prime and x² + x + 1 º 0 (mod q). Then x(x + 1) º -1 (mod q), and x² - x + 1 º -2x (mod q). Since x² + x + 1 is odd, q ¹ 2, then x² - x + 1 \not º 0 (mod q). Hence gcd(x² + x + 1,x² - x + 1) = 1.

: As we have seen from (b), x² + x + 1 is square if and only if x = -1 or 0. Indeed g(-1) = 0² and g(0) = 1². Otherwise, x² + x + 1 cannot be square. But gcd(x² + x + 1, (x + 1)(x² - x + 1)) = 1, so g(x) cannot be a square either. Hence x⁵ + x⁴ + x³ + x² + x + 1 is square if and only if x = -1 or 0.

: (e) Second solution. [M. Boase] Observe that x⁵ + x⁴ + ¼+ 1 = (x³ + 1)(x² + x + 1). Since x³ + 1 = (x² + x + 1)(x - 1) + 2, the greatest common divisor of x³ + 1 and x² + x + 1 must divide 2. But x² + x + 1 = x(x + 1) + 1 is always odd, so the greatest common divisor must be 1. Hence x² + x + 1 and x + 1 must both be square. Hence x must be either -1 or 0.

8.: First solution. Let BF = mBA, BD = lBC and CE = nCA.

: The conditions are that

l £ m £

and 1 - n £ 1 - m or m £ n .

We observe that [BDF] = lm[ABC].

: To see this, let BG = lBA. Then

[BDF] =

[BGD] =

l² [ABC] = ml[ABC] .

Similarly [AFE] = (1 - m)(1 - l)[ABC] and [DEC] = n(1 - l)[ABC].

: Hence

[DEF]

= (1 - lm-(1 - m)(1 - n) - n(1 - l))[ABC]

= (m- mn- ml+ nl)[ABC]

æ
ç
è

- (

- m)² -(m- l)(n- m)

ö
÷
ø

[ABC] £

[ABC]

with equality if and only if m = 1/2 and either l = m = 1/2 or n = m = 1/2. The result follows.

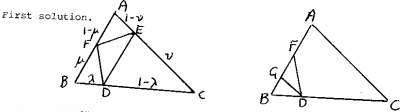
8.: Second solution. Let G be on AC so that FG || BC. Then, since [AE/EC] £ [AF/FB], E lies in the segment AG.

: Since [BD/DC] £ [BF/FA], DF produced is either parallel to AC or meets CA produced at a point X beyond A. Hence the distance from G to FD is not less than the distance from E to FD, so that [DEF] £ [FGD]. The area of [FGD] does not change as D varies along BC. To maximize [DEF] is suffices to consider the special case of triangles [FGD]. Let AF = xAB. Then FG = xBC and the heights of DDFG and DABC are in the ratio 1 - x. Hence

[DFG]

[ABC]

= x(1 - x)

which is maximized when x = ¹/₂. The result follows from this, with [DEF] being exactly one quarter of [ABC] when F and G are the midpoints of AB and AC respectively.

8.: Third solution. Set up the situation as in the second solution. Let BF = tFA. Then AB = (1 + t)FA, and the height of the triangle FGD is t/(1+t) times the height of the triangle ABC. Hence

[DEF] £ [FGD] =

(1+t)²

[ABC] .

Now

(1 + t)²

(1 - t)²

4(1 + t)²

³ 0

so that t(1 + t)^-2 £ 1/4 and the result follows. Equality occurs if and only if t = 1 and E = G, i.e., F and E are both midpoints of their sides.

9.: First solution. Let G be the circle of equation x² + y² = 1 and let l be the line of equation y = -1. The points of the square must lie on the circle of equation x² + y² = 2. Let them be

A ~ (Ö2 cosq, Ö2 sinq)

B ~ (-Ö2 sinq, Ö2 cosq)

C ~ (-Ö2 cosq, -Ö2 sinq)

D ~ (Ö2 sinq, -Ö2 cosq)

for some angle q with -p/4 £ q £ p/4. Observe that 1/Ö2 £ cosq £ 1 and that -1/Ö2 £ sinq £ 1/Ö2.

: Then A¢ ~ (Ö2 cosq, -1), B¢ ~ (-Ö2 sinq, -1), C¢ ~ (-Ö2 cosq, -1) and D¢ ~ (Ö2 sinq, -1), so that AA¢ = 1 + Ö2sinq, BB¢ = 1 + Ö2cosq, CC¢ = 1 - Ö2sinq and DD¢ = 1 - Ö2cosq. Hence

AA¢·CC¢- BB¢·DD¢

= (1 + Ö2 sinq)(1 - Ö2 sinq) -(1 + Ö2 cosq) |1 - Ö2 cosq|

= (1 + Ö2 sinq)(1 - Ö2 sinq) +(1 + Ö2 cosq)(1 - Ö2 cosq)

= 1 - 2sin² q+ 1 - 2cos² q = 0 .

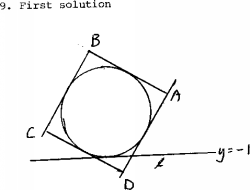
9.: Second solution. One can proceed as in the first solution, taking the four points on the larger circle at the intersection with the perpendicular lines y = mx and y = -x/m. The points are

A ~

æ
ç
è

Ö2

_____
Öm² + 1

mÖ2

_____
Öm² + 1

ö
÷
ø

B ~

æ
ç
è

-mÖ2

_____
Öm² + 1

Ö2

_____
Öm² + 1

ö
÷
ø

C ~

æ
ç
è

Ö2

_____
Öm² + 1

-mÖ2

_____
Öm² + 1

ö
÷
ø

D ~

æ
ç
è

mÖ2

_____
Öm² + 1

-Ö2

_____
Öm² + 1

ö
÷
ø

In this case, the products turn out to be equal to |(m² - 1)/(m² + 1) |.

9.: Third solution. [A. Birka] Let the circle have equation x² + y² = 1 and the square have vertices A ~ (1, 1), B ~ (-1, 1), C ~ (-1, -1), D ~ (1, -1). Suppose, wolog, that the line l is tangent to the circle at P (t, Ö[(1 - t²)]) with 0 < t < 1 and intersects CB produced in Y and AD in X. The line l has equation tx + Ö[(1 - t²)] y = 1 and so the coordinates of X are (1, u) and of Y are (-1, 1/u) where u = (1 - t)/Ö[(1 - t²)]. Now YB:YC = (1 - u):(1 + u) = AX:XD. Since DYBB¢ is similar to DYCC¢, BB¢:CC¢ = AA¢:DD¢, and the result follows.

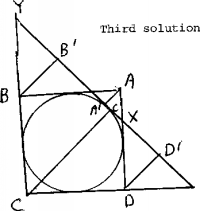
9.: Comment. If the circle has equation x² + y² = r², the square has vertices (±r, ±r) and the line has equation through a point (a, b) on the circle has equation ax + by = r², then the distance product is 2ab.

10.

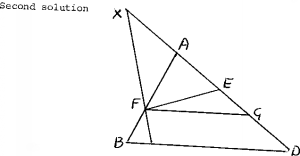
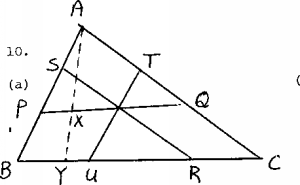
10.: (a) First solution. Recall that the centroid lies two-thirds of the way along the median from a vertex of the triangle to its opposite side. Let ABC be the fixed triangle and let PQ || BC, RS || AC and TU || BA, as in the diagram, with PQ, RS and TU intersecting in the centroid G.

: Observe, for example, that if X and Y lie on PQ and BC respectively, then AX:XY = 2:3. It follows from this that, if one ant is at A, then the centroid of the triangle formed by the three ants lies inside DAPQ (otherwise the midpoint of the side opposite the ant at A would not be in DABC). Similarly, if one ant is at B (respectively C) then the centroid of the ants' triangle lies within DBRS (respectively DCTU). Thus, if one ant traverses the entire perimeter, the centroid of the ants' triangle must lie inside the intersection of these three triangles, the singleton { G }. The result follows.

10.: (b) First solution. Suppose the vertices of the triangle are given by the planar vectors a, b and c; the centroid of the triangle is at ¹/₃(a + b + c). Suppose that one ant is placed at ta + (1 - t)b for 0 £ t £ 1. Place the other two ants at tb + (1 - t)c and tc+ (1 - t)a. The centroid of the ants' triangle is at

[(ta + (1 - t)b) +(tb + (1 - t)c) + (tc + (1 - t)a) =

(a + b + c) .

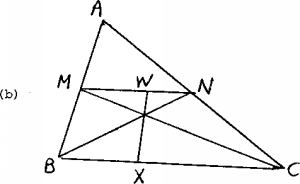
: (b) Second solution. If one ant is at a vertex, then we can replace the remaining ants at the other vertices of the fixed triangle. Suppose, wolog, the ant is at X in the side BC.

: Let MN be the line joining the midpoints M and N of AB and AC respectively; MN || BC. Let XG meet MN at W. Since BG:BN ( = CG:CM) = 2:3, it follows, by considering the similar triangles BGX and NGW, that XG:XW = 2:3. Hence the midpoint of the segment joining the other two ants' positions must be at W. Thus, the problem now is to find points Y and Z on the perimeter of DABC such that W is the midpoint of YZ. We use a continuity argument.

: Let UV be any segment containing W whose endpoints lie on the perimeter of DABC. Let Y travel counterclockwise around the perimeter from U to V, and let Z be a point on the perimeter such that W lies on YZ. When Y is at U, YW:WZ = VW:WV, while when Y is at V, YW:WZ = VW:WU. Hence YW:WZ varies continuously from a certain ratio to its reciprocal, so there must be a position for which YW = WZ.

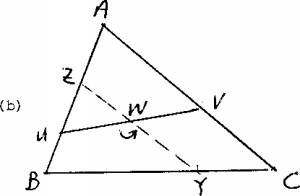
: (b) Third solution. [A. Panayotov] Suppose that the triangle has vertices at (0, 0), (1, 0) and (u, v), so that its centroid is at (¹/₃(1 + u), ^v/₃). Wolog, let one ant be at (a, 0) where 0 £ a £ 1. Put the second ant at (u, v). Then we will place the third ant at a point (b, 0) on the x-axis. We require that ¹/₃(a + b + u) = ¹/₃(1 + u), so that b = 1 - a. Clearly, 0 £ b £ 1 and the result follows.

11.

11.: First solution. We first establish that we must have AD = BC, AB = CD and AC = BD. This is obvious if the triangular faces are equilateral. Suppose that DABC is isosceles with AB = AC ¹ BC. If AB = AD, when BC = BD and DBCD would fail to be congruent to DABC. Hence AB = AC = BD = CD. Suppose DABC is scalene. Since DABC º DABD, AD must be equal to one of AB, AC or BC. Since DABD and DACD are not isosceles, the first two possibilities are excluded and so AD = BC. The other cases follow similarly. 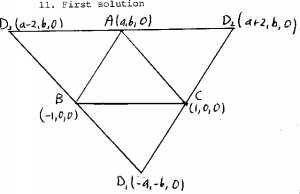Fold out the tetrahedron flat to the configuation of the diagram.

: Wolog, we can assign coordinates

A ~ (a, b, 0) B ~ (-1, 0, 0) C ~ (1, 0, 0)

D₁ ~ (-a, -b, 0) D₂ ~ (a + 2, b, 0) (a - 2, b, 0)

with a, b positive. Since the D_i swing up to D about the hinges BC, CA, AB, D must lie vertically above a point E in the (x, y)-plane for which D₁ E ^BC, D₂ E ^AC, D₃E ^AB. This point E is given by

E ~

æ
ç
è

-a ,

2a² + b² - 2

, 0

ö
÷
ø

so that, for some value of t,

D ~

æ
ç
è

-a ,

2a² + b² - 2

, t

ö
÷
ø

Using the fact that |AD | = 2 and |CD | = |CD₁ |, we find that

bt² = 4(1 - a²)(b² + a² - 1) = 4(b² + 2a² - 1 - a²b² - a⁴) .

We check that the quantity on the right is indeed positive. Note that each angle of DABC is acute. For if ÐA ³ 90^°, then ÐD₃ AB + ÐD₂ AC £ 90^° and D₃A and D₂A could not fold up to coincide in a point above the plane. Since ÐB < 90^° and ÐC < 90^°, A lies outside the circle diameter BC. Hence a² < 1 and a² + b² > 1.

: Now BC = 2(1, 0, 0),

AD = 2

æ
ç
è

-a,

a² - 1

_____________
Ö(1-a²)(b²+a²-1)

ö
÷
ø

and |AD | = |BC | = 2. Hence

cosa =

BC·AD

|BC ||AD |

= -a .

Also sin(B+C) = sinA, so, by the Law of Sines,

sin(B-C)

sin(B+C)

æ
ç
è

sinB

sinA

ö
÷
ø

cosC-

æ
ç
è

sinC

sinA

ö
÷
ø

cosB

|AC |

cosC -

|AB |

cosB

(1 - a) - (a + 1)

= -a = cosa .

[Note that |AC |cosC is the length of the projection of AC onto AB, namely 1 - a.]

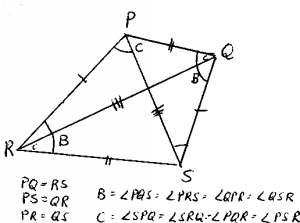
11.: Second solution. [A. Chan] Let PQRS be the tetrahedron. PQ = RS, PS = QR, PR = QS. Let B = ÐPQS = ÐPRS = ÐQPR = ÐQSR and C = ÐSPQ = ÐSRQ = ÐPQR = ÐPSR. Then

|PQ |·|SR |cosa

= PQ ·SR = PQ ·(PS - PR)

= PQ ·PS - PQ ·PR

= |PQ ||PS |cosC - |PQ ||PR |cosB .

Therefore

|SR |cosa = |PS |cosC - |PR |cosB .

By the Law of Sines,

|PR |

sinC

|PS |

sinB

|SR |

sin(B+C)

whence

|SR |cosa =

|SR |sinB cosC

sin(B+C)

|SR |cosB sinC

sin(B+C)

= |SR |

sin(B-C)

sin(B+C)

The result follows.

11.: Third solution. [I. Panayotov] Assign coordinates A ~ (u, v, 0), B ~ (0, 0, 0), C ~ (p, q, r) and D ~ (w, 0, 0). Let |AD | = |BC | = a, |BD | = |AC | = b and |AB | = |CD | = c. Suppose that a is the angle between AD and BC.

a² cosa = (u - w, v, 0)·(p, q, r) = pu - pw + qv .

Let B = ÐABC and C = ÐCBD = ÐBCA. Then

ac cosB = (u, v, 0)·(p, q, r) = pu + qv

and

ab cosC = (w, 0, 0)·(p, q, r) = pw .

Then

a² cosa- ac cosB + ab cosC = 0

whence

a cosa

= c cosB - b cosC

a sinC cosB - a sinB cosC

sinA

a sin(C - B)

sin(C+B)

12.

12.: (a) First solution. (a, b) = (3, 2) yields 2a - 1 = 5, 2b - 1 = 3 and a + b = 5; (a, b) = (3, 4) yields 2a - 1 = 5, 2b - 1 = 7 and a + b = 7. Suppose that a and b are primes. Then for a + b to be prime, a + b must be odd, so that one of a and b, say b, is equal to 2. Thus, we require the a + 2 and 2a - 1, along with a, to be prime. This is true when a = 3.

: Now suppose a is an odd prime exceeding 3. Then a º ±1 (mod 6), so the only way a and a + 2 can both be prime is for a º -1 (mod 6), whence 2a - 1 º -3 (mod 6). Thus, 3 divides 2a - 1, and since 2a - 1 ³ 9, 2a - 1 must be composite.

12.: (b) First solution. We first recall a bit of theory. Let p be a prime. By Fermat's Little Theorem, a^p-1 º 1 (mod p) whenever gcd(a, p) = 1. Let d be the smallest positive integer for which a^d º ±1 (mod p). Then d divides p-1, and indeed divides any positive integer k for which a^k º ±1 (mod p). Now to the problem.

: Since a + b is prime, a ¹ b. Wolog, let a > b and let p = a + b. Then a º -b (mod p), so that

a^b + b^a º (-b)^b + b^a º b^b((-1)^b + b^a-b) .

Suppose, if possible, that p divides a^b + b^a. Then, since b < p, gcd(b, p) = 1 and so b^a-b º (-1)^b+1 (mod p). It follows that

b^2b-1 = b^(p-1)-(a-b) º (-1)^b+1 mod p .

Now 2b - 1 is prime, so that 2b - 1 must be the smallest exponent d for which b^d º ±1 (mod p). Hence 2b - 1 divides a - b, so that for some positive integer c, a - b = c(2b - 1), whence a = b + 2bc - c and so

2a - 1 = 2b - 1 + (2b - 1)2c = (2b - 1)(2c + 1) .

But 2a - 1 is prime and 2b - 1 > 1, so 2c + 1 = 1 and c = 0. This is a contradiction. Hence p does not divide a^b + b^a.

: Similarly, using the fact that a^b + b^a º (-b)^a + b^b º b^b ((-1)^a b^a-b + 1), we can show that p does not divide a^a + b^b.

: (b) Second solution. [M. Boase] Suppose that a and b exist as specified. Exactly one of a and b is odd, since a + b is prime. Let it be a. Modulo a + b, we have that

0 º a^b + b^a = a^b + (-a)^a º a^b - a^a º a^a(a^b-a - 1) or a^b(1 - a^a-b)

according as a < b or a > b. Hence a^{|b-a |} - 1 º 0 (mod a + b). Now a + b - 1 ±|b - a | = 2a - 1 or 2b - 1, and a^{a + b - 1} º 1 (mod a + b) (by Fermat's Little Theorem). Hence a^{2a - 1} º a^{2b - 1} º 1 (mod a + b). Both 2a - 1 and 2b - 1 exceed 1 and are divisible by the smallest value of m for which a^m º 1 (mod a + b). Since both are prime, 2a - 1 = 2b - 1 = m, whence a = b, a contradiction. A similar argument can be applied to a^a + b^b.

: (c) Third solution. Suppose, if possible, that one of a^b + b^a and a^a + b^b is divisible by a + b. Then a + b divides their product a^a+b + (ab)^a + (ab)^b + b^a+b. By Fermat's Little Theorem, a^a+b + b^a+b º a + b º 0 (mod a+b), so that (ab)^a + (ab)^b º 0 (mod a + b). Since a + b is prime, it is odd and so a ¹ b. Wolog, let a > b. Then

(ab)^a + (ab)^b = (ab)^b[(ab)^a-b + 1]

and gcd(a, a+b) = gcd(b, a+b) = 1, so that (ab)^a-b + 1 º 0 (mod a + b). Since (ab)^a+b-1 º 1 (mod a + b), it follows that (ab)^2a-1 º (ab)^2b-1 º -1 (mod a+b). As in the foregoing solution, it follows that a = b, and we get a contradiction.