Next: Henri Darmon - Modularity Up: Number Theory / Théorie Previous: Number Theory / Théorie
A. Akbary - On the distribution of the values of symmetric square
L-functions in the half plane
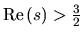
| A. AKBARY, Department of Mathematics and Statistics, Concordia University, Montreal, Quebec H3G 1M8, Canada |
| On the distribution of the values of symmetric square
L-functions in the half plane
|
Let
Lsym2(f)(s) be the symmetric square L-function
associated to a newform of weight 2 and level N. We will derive an
asymptotic formula for the average values of
Lsym2(f)(s) at a
point s0 in the half plane
. Assuming the
Riemann hypothesis for the Riemann zeta function, we are able to
extend
our result to the half plane
.
