Stephen D. Theriault - Homotopy exponents for certain 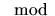-2^r Moore spaces

STEPHEN D. THERIAULT, Department of Mathematics, MIT, Cambridge, Massachusetts  02139, USA

Homotopy exponents for certain -2r Moore spaces

For a prime p, the -p^r Moore space P^m(p^r) is the cofiber of the degree p^r map on S^m. A special case of Barratt's conjecture is that if then the p-primary torsion in is annihilated by p^r+1. It is well known that this is true when p is an odd prime. We investigate to what extent it is true when p=2 and .